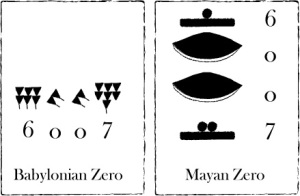
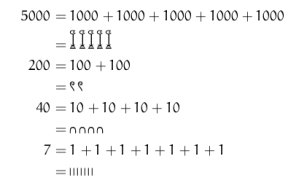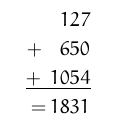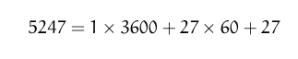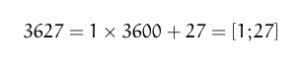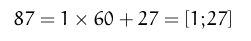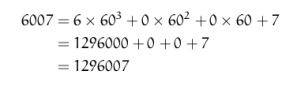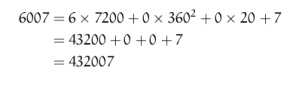Pride and Prejudice
As a part of the graduate courses we had to do a few presentations. During the course on sociology of education I reviewed a book Prejudice and Pride by Krishna Kumar. When I was first told about the book I was not too keen to do the review, as the title suggested nothing about the content of the book. But when I was told about the synopsis of the book I became immediately interested. So what is this book with a title made by rearranging the title of another famous book by Jane Austin about. So we will first talk about the subject matter of the book.
What this work is about?
As the back cover of the book says it is a comparative study of the modern representations of modern history in Indian and Pakistani textbooks. The book consists of an inquiry into the perceptions of the past that the Indian and Pakistani children encounter at the school. So the book is about the kind of history being taught in the schools to children in India and Pakistan. So we being the children and product of such an education do differ from our Pakistani counterparts in our view of history.
History as it is known is seen by different people differently. For some heroes are villains and vice-versa if change the sides of a given conflict. Thus for us Indians the British officers who established and firmed the British rule in India would be villains whereas for the British they were heroes. So to form an objective view about the history of a particular event is very difficult if not impossible. One of the reason for this is the fact that we depend upon historical evidences for building the image of the past. These evidences may be in form of reports, books or other works and folk tales about that particular event. Thus we will be most of the time biased and subjective about the information that we have to build upon the image of the past we have. It will be no wonder that the images of the past that are familiar to us, are at times starkly different from those brought in a different culture.
In general there is gloom in the education systems of both the countries. India is no more better off than Pakistan in general in the education field. The subject matter of this work in particular is the history as taught in the two countries. In a sense there is an absence of academic curiosity in both the countries towards each other. We have no ‘experts’ in India on Pakistan and likewise for Pakistan. Compare this with the experts that the USA and the former USSR had for each other during the cold war era. There were entire think-tanks dedicated to know about the ‘other’.
In case of India and Pakistan, both the countries live under the impression that they know each other. This emanates from the fact that the ‘other’ is, after all, a former aspect of the ‘self.’ India and Pakistan are politically so far apart, but, geographically and culturally so close that there is no room for an epistemic space between them. This makes us believe that we know the ‘other’ too well.
One of the roles of education in the modern states in the world is imparting a sense of national identity. The children are indoctrinated via history to have a ‘nationalist’ character. So history as taught in the schools takes the burden of nation building than any other subject that is taught. One of the roles of history to arouse the interest of the young in the past and to inculcate a respect for it is sidelined in modern day India and Pakistan. Whatever debates that are present in India and Pakistan on the teaching of history are political and not pedagogic. The pedagogic uses and role of the subject of history has been given up for the more important role of history as tool for nation building.
Why the modern history?
The author choose to concentrate on the modern history of the sub-continent. The ‘modern’ is meant to connote here the era from 1857 to the freedom and formation of the two nation identities in 1947. The older history of the sub-continent is more controversial in the sense that the views that are portrayed by the history as taught in the two nations are radically different. ‘Invaders’ in India are seen as ‘heroes’ in Pakistan. No wonder that even the modern history of the two nations is subject to the bias of the respective countries.
What most people and more importantly the young children don’t realise that there is always another view of the history, through which the now familiar events look totally alien to us. When we come across such histories there is a sense of
jamais vu involved. Suddenly the things so well known to us are entirely changed in terms of the perspectives. Also the events that we think are important with respect to the history that we are taught, would be trivial in some other histories.
Modern history has greater potential to for engaging children in activities connected with the study of the social sciences than the history of other periods has. So this has the potential to establish the modern period as a subject matter for advanced studies. It will help promote a better understanding between India and Pakistan by helping readers in both countries to grasp how a common recent past is looked by the other.
In this case the researcher being an Indian the impartiality of the researcher demanded great self restraint and imagination on the part of the researcher. Unknowingly the researcher would be biased in forming the opinions which are so ‘clear and simple’ for us. So one of the major objectives of this study is to examine the rival ideologies of nationalism into which schools attempt to socialize the young. Another objective being a probe into the politics of history writing as a means to understand the contribution that schooling makes to the Indo-Pak conflict.
Many things that come out of this study are interesting and I was surely taken aback by some of them. The familiarity that we have with the events of the past is lost when we take the `other’ perspective into account. The study was based on the sample of textbooks taken from both the countries. The Pakistani text books that formed the part of the study were both privately published and published by the various state boards. The regional variation in the text books of Pakistan was found to be much less than than in India. The Indian sample consisted of the books by various state boards, ICSE and NCERT and CBSE.
The Challenge of The Past
In this section we discuss the cognitive challenge that teaching history at school might present to children. Before coming to the school the children have some tacit knowledge about the past. By primary socialization it is meant the induction of the child in the society. When the children are introduced in the society they are taught the customs, practices and norms of the society that they are going to be a part of. During this a certain amount of knowledge is essentially passed on to the children, which helps them form an identity for themselves in the contemporary society that they are a part of. So by the time children go to school they have acquired the basic deeper imprint of membership of a society as an outcome of primary socialization.
The school thus gets a child with the basic notions already formed, and these are very difficult to change in the school. The school has no option but to work with the personality of the child thus formed. The schools are seen as instruments of cultivating loyal citizens. And in the secondary socialization the children are socialized into an ‘approved’ past. This ‘approval’ is from the state. Also the difference between the awareness and knowledge is quite often blurred for the children. For example consider the statement
India gained independence from the British rule on 15th August 1947.
Now just to ‘know’ this information as a matter of fact is quite different from having a deeper knowledge about the notions of independence, rule etc. Almost all people know this, but how many of them can actually understand the meaning of a sentence like this, when it is translated in terms of the events, people and the circumstances that were present at that point of time. Events which occured in the past require us to appreciate the circumstances, values and choices that shaped the people who were involved
To analyze historical events we need to go into a time frame without being completely submerged in it. By this it is meant that we have to see the ‘past’ in terms of the ‘past’. We should not cannot impose the contemporary beliefs, thoughts and values on the people and the events of the past, because if we do that we might loose the view that the people of the past had. Thus the cognitive challenge that history presents is certainly great and it requires much more processing on the part of the learner who is presented with the facts of the history. For in history each event has to be seen in dual mode:
- The given event as the outcome of the events preceding it.
- The given event as the cause of events following it.
Thus for example when we see the rebellion of 1857, we have to see it in the light of the events that caused it, and at the same time we also have to see it in the light of the events that it caused. How we see a particular event would strongly depend on what framework of history we already we have. The most natural way for us to see any event is to fit it in the framework that we already possess. Also anomalies, if any, are usually ‘interpreted’ in a way to fit the framework. Changing the framework itself is very difficult even for the adults and I guess almost impossible for the children. For example if we are told that ‘Gandhi was not at all important for the freedom from the British,’ then how are we going to react? We have been always ‘told’ that this is so, so we believe it. The point that I want to make here is not just about the role of Gandhi’s involvement in the freedom struggle, but rather just to give the reader a taste of what change in the framework could result in.
Coming back to the two positions that a reader in history has to take into account, cognitively what is requirement for making such conjectures? This requires on the part of the children the capacity of reversibility. The reversibility as defined here is the reversibility of the Piagetian tasks. Piaget places the ability of the reversibility in the concrete operational period of his framework of cognitive development.
One of the ways in which the reversibility can manifest in the children is reversibility of thought.
The children thus have two main difficulties that they face when they are learning history in the school. One of them is cognitive and the other is sociological plus cognitive. The impact of culture upon the image of the past that we have is tremendous, and this is particularly true for children. A child can be often presented with a version of history as a part of primary socialization, which is not the one which is ‘approved’ by the state. The popular social memory both in India and Pakistan about the events in the past shapes the framework of the children, according to which they try to make sense of the facts presented to them later. In this case it will directly conflict with the knowledge that is presented in the school. For example if a child is told at the home that ‘Great unjustice was done only to Hindus during the partition’, then this is certainly going to conflict with the ‘approved’ version of the history being taught at the school. This is what I call the sociological plus cognitive problem that the children face. How can something be true and also be non-true at the same time? This I guess is not only a problem with children but also [more] with adults. The notion that there is only one truth, and that is what I believe in, the rest are propaganda’s seem to fit the right wing frameworks present in both the countries. The very idea of reality can be seen in a different light is not acceptable to most of us. Why? Because we don’t want to be in a world where we cannot understand something that is not the part of our standard framework.
The other major problem that the children face is cognitive. This relates to the fact that how much the teaching of history at school attunes itself to the cognitive levels of the children. As we have seen the interpretation of historical events requires a notion of reversibility on the part of the learner, how many text books address this fact, or even take into account this. As in India so in Pakistan the role of history as a subject is seen more as a subject to be passed than anything else. The pattern of rote learning the subject without understanding the complexities of the issues involved, seems to be the idea of doing history in both the countries. More emphasis is on the ‘knowledge’ part than on ‘awareness’ of the subject at hand.
Also as far as the ‘good’ careers are concerned the subject of history is taken over by more fruitful subjects of mathematics and sciences. So history is just seen as an auxiliary subject which has to be passed, and which can be passed without understanding, because it is not going to help you in the future to secure a ‘good’ career.
Frames of Popular Perception
In this section as title suggests we will focus on the frames of perception by which the general population forms a framework so as to understand the past. For this we have to understand the notion of the ‘other’. What is meant by the ‘other’? In both India and Pakistan the past is intertwined with the current and evolving perceptions of the ‘other.’ Our own national identities are seen in the frames of perception by hinting at the ‘other’. Each side has something of the other in it. Each country presents a strong case of dependence on the ‘other’ for defining itself. Thus question can be raised that ‘If Pakistan is an Islamic state how can India be a secular one?’ For if India were a truly pluralist society there would not be any need for Pakistan. We see that India’s portrayal as a ‘secular’ society as opposed to an ‘Islamic’ one in Pakistan is exactly this. We need to contrast ‘our’ nation with ‘their’ so as to prove our identity.
I liked this part of the book very much. It really shakes you and your perception about the past. So what this essentially means is that there is a Pakistan which we Indians may not have the epistemic means to fathom and same is true for a resident of Pakistan for India. It really provides you with a clue of how hard it is to let go the perceptions we already have. As for the case in Pakistan education there has succeeded in dissociating partition from its painful violent reality and has in turn converted it into an achievement for all Pakistanis. The very idea that India does not accept Pakistan’s existence and Pakistan poses no real challenge for India are the two sides of the same emotion. The point that is being made here is that do define the very concept of Pakistan as a nation in the past and in the current times, the perception of the ‘other’ is being taken into account. Thus the national self awareness is also determined by reference to the ‘other.’
For case of India the event of Partition is seen as an inevitable turn of events. While the current view of Pakistan is in terms of an active supporter of terrorism. Also due to the unstable democracy in Pakistan a view is that [I somehow liked it very much] ‘An army looking for a country’. Most of the Indian perception about Pakistan is derived from pre-partition memory and the wars that followed with Pakistan. Thus we see that the notion of the ‘other’ is interwined with our past as well as our present.
Ideology and Textbooks
The state in both the countries wants to present its ‘approved’ version of the history to children to inculcate in them the qualities of an ideal citizen of the given state. No wonder that the history as seen in the different frameworks will be different. In this approach the textbooks are instrumental, and this is a direct descendant of the colonial past. Under the British rule in the sub-continent the history was presented in a version that was ‘suitable’ for the administrators. In case of India the Kothari Commission showed willingness to turn nation building into an ideology and to see the education as a prime instrument to propagate it. In India there is a leftward tilt, with the political ideology being essentially modernist and progressive, while pedagogically it is conventional in character. Why this stark contrast in the philosophy and the pedagogy of the history being taught is the question that we want to ask. This is partly because it suits the state ideology so.
In the case of Pakistan the urge to define and construct Pakistan as an Islamic nation occupies the central place in the system. The concern for national identity of Pakistan occupies form of an obsessive mission, for which ‘evidences’ are seen throughout the history of the modern era. Thus ideology is used in Pakistan to indicate a rationale for self identity.
In India recent trends to ‘color’ the content have been started, against the official policy to propagate a secular version of the nation. The colonial past gives a common heritage to both the countries in terms of the central control over what is taught and how it is evaluated. In both the countries the prescribed textbooks form the de facto curriculum. Questions like
In what way did the revolt of 1857 influence the nationalists during the struggle for freedom?
which do appear in exams relate to the fact that there is a way in which the revolt influenced the nationalists and this is the way which you are supposed to know and write about. Does this not destroy the notion of history itself, for the facts themselves can be evaluated in terms of framework you see them in.
I cannot help here but to bring from the philosophy of science the notion of ‘theory ladenness of data.’ This is one of the factors which led to the downfall of the Logical Positivists, in the late half of 20th century. What this essentially means is that whatever observations that we have, can be interpreted by us only in the terms of the theory that we are working with. This is something which you cannot do away with. The Logical Positivists on the other hand believed in the exactly opposite thing. They thought that the observations presented an objective truth which can be evaluated without any reference to theories. But this I guess is a normative position than a descriptive one as regards to the science. This view is obsolete in the philosophy of science and now philosophers do believe in the theory ladenness of data. More cannot be said to be true about the subject of history itself. Though it took some time for the philosophers of science to realize, this has been always the case with history. The notion that science is objective in terms of the outlook, unlike history was abandoned.
Here I cannot but restrain myself from giving example from George Orwell’s 1984, where in Ministry of Truth’s dictum says:
Who control the past, controls the future.
Who control the present, controls the past.
Is this not what our governments are doing? The more I think about this more I am convinced that our present state has the form of the Orwellian state. Where in the past is rewritten so as the state is always right. The difference being that our textbooks were written once and have been propagating the same stories since then. Is not the state trying to control the future, in terms of the citizens that are being made by the education that is imparted to them. This I guess is the Nehruvian vision, where the educated elite are supposed to keep out of politics. Politics in most of the ‘good’ families is seen as a ‘dirty’ game, where people from ‘good’ families should not get involved. But does not the history stand against evidence to the fact that almost all of the people who were involved in the freedom struggle were from ‘good’ families. During the freedom struggle it was a prestige to be involved politics, but what has changed in the years in between so that the roles are reversed. What the education has succeeded in doing in India, is to dissociate the learned elite from the actual political situation in the country. Is this not the state at work?
Rival Histories
Now we come to the main part of this work, the rival histories that the school children of the two countries are being presented with in the schools. The words and events which have a common meaning in one country have totally different in the other. The very word freedom has different meaning for both the countries, India ‘woken up,’ whereas Pakistan was ‘born.’ Here again I would like to borrow an idea from the philosophy of science; Kuhn’s idea of incommensurability. The basic idea is that different theories or paradigms can be hard or impossible to compare, in a properly unbiased way. Thus when we see the different events in modern history, in the two different paradigms of the two states, they no wonder appear to be entirely different. To say that one version is correct and another a distorted version of it, is to loose the whole point so what is being said here.
The memory of the struggle with the British has great memory for both of the newly born nation states of India and Pakistan. The emergence of the national identity forms a central theme in the histories of both the nations. For the consolidation of the nation state, this memory needs to be preserved and passed on to the next generation. Only then the nation state will be successful, otherwise be in demise. Thus the state itself works towards its own growth and welfare, just as The Party in 1984. This is done for the respective nations by recasting the record of their freedom struggle into a narrative for the young.
Hence we
have two prototypes of the same event, one which serves the interest of each nation state. Thus were born the two ‘master narratives’ for the two nation states. But the question is, should they be the same? In both the states the school historians take the ‘national’ and ‘approved’ stance on the past.
So what is the framework in which this evaluation is done in? In this work, three themes have been explored in the context of the material presented in the textbooks of the two nations.
- Politics of mention: By politics of mention it is meant the decision to include or exclude a particular name or event in the discourse of history. This in turn is directly influenced by larger process of identity building.
- Pacing of the end:Both the systems have a different pacing towards the end of the struggle. The aspect of story telling having many linkages to the politics involved, but it also has to do with nature of educational system, how it treats knowledge as a body of fact. More attention is given to the individual facts, rather than to the connections between them. Also there is a rapid movement between events, without ascertaining the causal relationships if any between the end.
-
Conception of the end: Both the narratives come to a stop in 1947. The end point is conceptualized very differently in the two master narratives. For the Indian master narrative the freedom and partition is seen as a great achievement, along with terrible sense loss and sadness, and a sense of failure to subvert a conspiracy is embedded. Whereas in case of Pakistan it is seen as a remarkable achievement, which is somewhat mitigated by a sense of injustice. For the Indian master narrative the history starts in ancient times and comes to an end in 1947. And in case of Pakistan, the ‘end’ marks formal beginning of the nation state called Pakistan. In fact the history of Pakistan starts from 1947.
Blurred Divergences
With the given animosity present between the two countries we would expect that the histories present in the textbooks would be mirror images of each other. But this is not the case, the two narratives are related but in a highly complex manner. Both the narratives follow a path which see to it that the events and persons mentioned the master plan of each. It is not that eminent personalities are portrayed as villians in the other history. Both focus on ‘high’ politics rather than social dynamics; decisions taken by eminent leaders and British administrators. The freedom struggle is treated as an allegory, composed for the purpose of reminding the young that they are inheritors of great storehouse values. One of the epistemological difference between the two versions is that the Pakistani version focuses more on ‘how’ was freedom achieved and the Indian narrative focuses on ‘why’ it had to take the form it did.
A Beginning Located
So what is the starting point in both the master narratives? Both the master narratives take the Rebellion of 1857 as a starting point of the route to freedom, which ends in 1947. The textbooks of both sides convey the impression that rebels were inspired by a dream of national independence. But the words such as ‘national’ or ‘nationalist’ are not qualified and are not cautioned against. The very fact that these notions do not apply in that era as they apply now is seem to have been forgotten by the writers on both the sides. So we come to a question of whether there was there any ‘nationalism’ in the revolt of 1857? Most of the Indian writers answer this question positively, and see the revolt as the ‘first war of Indian independence.’ As of now there is not any clear consensus on the issue. One of the ironies that the revolt presents is that of the so called ‘rebels’ and the ‘educated Indians.’ Whereas the rebels are presented to be against the British, the reasons cited are political and religious, whereas the various religious and social reformers who were contemporaries of the same rebels are presented in an entirely different light. What is forgotten that the very reformers which have supposed to lay the seeds of the social enlightenment in India were very supporters of the British rule.


Children [and I guess even most adults] are not allowed to realize that events of 1857 look remarkably different from different perspectives. In the Pakistani textbooks the events of 1857 have to be placed as the formal beginning of the master narrative. 1857 is seen as an attempt by the Muslim rulers to throw away the British rule and re-establish Mughal rule; attention is brought to the fact that Muslims as a community were willing to fight for rights and status. So who according to the narratives are the heroes of 1857? The Indian narrative answers in plural as
Mangal Pandey, Rani of Jhansi, Tatya Tope, Bahadur Shah Zafar, Nana Saheb. But in case of the Pakistani texts the discussion of 1857 is not elaborated much. For any elaborate discussion on 1857 would show that Muslims and Hindus were capable of fighting as an unified force, and this would certainly not fit in the master narrative of Pakistan. For Pakistani writers any pedagogic narrative should serve a dual role; it should describe how the colonial rule ended and should also explain how Pakistan came into being. So this represents a problem for the writers of ‘Pakistan Studies.’ The other dilemma is in the structure of the narrative itself. One of the key figures in the start of the Pakistani master narrative is Sir Sayyid Ahmad Khan, who is presented as a ”great hero” and sided with the British during 1857. So how will Pakistani writer solve a dilemma like this:
If it is a war of independence waged by the Muslims against the hated British foreigner, how can Sir Sayyid Ahmad Khan, who sided with the British and condemned the native rising be presented to the students as “great hero” and “the greatest thinker of Pakistan?”
So what do we make of this? The events in 1857 can be seen as a last convulsive movement of protest against the coming of west on the part of traditional India. Though the revolt did have great influence on the subsequent struggle, it is hard to say that it was in any logical way connected to this struggle. In both the narratives the scale of the violence that took place in the revolt remains vague. Why should be this so? This is an unanswered question.
Both in character and content the topic of national character contrasts sharply with the revolt of 1857. The textbooks even at the lower classes attempt to convey to children a notion of the reform movements; terms like ‘tradition’, ‘progress’, and ‘reform’. But how much of this the children are cognitively capable of learning is a question. I guess even how many adults can understand these notions. For the Pakistani writers the aim is to impart the ability to ‘understand the Hindu and Muslim differences and the resultant need for Pakistan’. Whereas for the Indian writers the idea of secularism has to take root in the nineteenth century reformers. Hence they are said to be ‘deeply influenced by the ideas of rationalism and humanism and of human equality’.

We now take a look at the presentation of Sir Sayyid Ahmad Khan in the two narratives. In the Pakistani master narrative he is the key figure post 1857 and most of the attention is on the Aligarh movement. The foundations of the Pakistani Master Narrative are established in this era. The categories ‘Hindus’ and ‘Muslims’ are constructed, with some stereotypes accommodating the master narrative. The ‘Hindus’ are given certain essential unalienable properties which are supposed to the part of their nature. They are supposed to be cruel, manipulative, unreliable.
The idea that there was a tacit understanding between the Hindus and British to undermine and rule the Muslims runs through the master narrative. Thus Muslims are seen as the oppressed lot who rose for themselves to create a separate state. Sayyid Ahmad Khan is presented in Pakistani textbooks as solitary person ahead of times; a great leader and a visionary and most importantly who introduced the idea of two nation theory. Though he is verbalized as a great man; he is a as a tool to stigmatize Congress. The connotations that Congress has are that it was a pure Hindu body, and it is used to stereotype Hindus as selfish and sectarian people.
In the Indian narrative on the other hand Sir Sayyid Ahmad Khan he is just one of the many reformers that are present during that era. Three major themes of his work are covered in the the textbooks of both sides. They are:
- Conciliatory view of the British.
- Caution against representative democracy and Congress.
- Institutional work to promote Western Education among the Muslims.
But only the last one is emphasized in the Indian textbooks, so that he becomes just one of many. The special status that is awarded to him in the Pakistani context is absent in the Indian context.
Tools that are required to read into the cultural awakening are not presented to the students. Even if somebody wants to understand the meaning of the terms involved there is no potion but to memorize.
When one reads the texts the unfortunate impression is given that Congress was set up in one day, with clear cut aim for the liberation of India from the British rule. Just as the anti-Hindu sentiments run throughout the Pakistani master narrative, the idea of ‘Divide and Rule’ by the British runs throughout the Indian master narrative. The partition of Bengal on the religious lines is an example of this. But in the Pakistani master narrative Jinnah’s participation in the Congress during the Bengal movement period is suppressed in the Pakistani texts as it does not fit their master narrative, in which Congress is a purely Hindu body and primarily anti-Muslim.
The formation of Muslim league is presented as if it was a natural outcome of the conditions present then. Since the Congress was a purely Hindu body, the Muslims were left with no political organization of their own. So to make the voice of the Muslims to be heard the formation of a Muslim political organization was the only alternative left. The Muslim League was formed as a result. The Muslim League thus steps out of history assuming the status of quasi-divine mechanism that Muslims of India always needed. The formation of the Muslim League is presented as culmination of social and political awakening of the Muslims. On the other hand in the Indian textbooks the creation of the Muslim League is seen as another version of the ‘Divide and Rule’ policy of the British. Thus we see that how one event viz. the formation of the Muslim League ‘fits’ properly in both the master narratives, which have their own agenda of reaching the summit in 1947.
Unity and Breakup [1916-1922]
Even though there were basic ideological differences present in the view points of Congress and the League some sort of communal harmony was present during the events leading to the Khilafat and the Non-Cooperation Movements. So we see now this era of harmony between the two political parties is portrayed in the two textbooks. It is at this juncture that Gandhi enters the political scene in the Indian narrative. As he became the leader of the national movement, the movement is transformed. The transformation of the movement was in terms of the class and the region of the people participating in the movement. Thus the movement became a mass movement due to arrival of Gandhi, and he is seen as a hero in the Indian context. Contrastingly in the Pakistani texts Gandhi is characterized as a ‘Hindu leader.’ The significance of Gandhi’s entry into politics is reduced significantly. The very fact that during this period the freedom of Pakistan depended so much on the freedom of India is oblivious to the writers [and hence to the readers] in Pakistan.
The Khilafat Movement
In the Indian context the Khilafat movement marks the high point of Hindu-Muslim unity. This incidence is always seen in a secular light, hence the triumph of secularism is seen as a guiding value of national movement. The Khilafat movement is to be seen as ‘golden opportunity for cementing Hindu-Muslim unity and bringing the Muslim masses into national movement‘. On the other hand for Pakistani writers Khilafat along with Hijrat, is remarkable for the fact that Hindus and Muslims worked jointly for their success, but this could not continue because of `the hostile attitude of the Hindus toward Muslims became evident.‘ Also the idea of anti-Muslim sentiment runs throughout the narrative. This statement reveals this idea; `It is obvious that no Hindu could be seriously concerned with whether Khilafat was to survive or not.’ In the Pakistani texts the Jinnah’s opposition to Khilafat movement is suppressed, as this would not fit the master narrative in the light of the later events. Maybe somebody should raise a question: How can Quaid-e-Azam oppose the Khilafat movement which was so dear to the Muslims?
As far as the Pakistani narrative is concerned Gandhi is presented as a shrewd character who used the Khilafat movement for attaining his goals. The fact that Gandhi called off the Movement after the Chauri-Chaura incident is portrayed as a decisive moment in Muslims organizing themselves instead of looking for allies. Whereas in the Indian context Gandhi’s role is unique and has three broad dimensions:
- A mass leader.
- An imaginative strategist.
- A social reformer.
Gandhi is the superman of Indian politics, he can do no wrong. The status that Gandhi achieved remains a mystery, so do the reasons for choices he made. There is no way the readers can understand the political games that were played, in the era, as only facts without much interpretation is presented. As far as Gandhi is concerned in the Indian narrative, politician in him is left out; only Mahatma remains. One of the basic premise of Gandhian thought that substituted the value of loyalty to state by self imposed structure of moral behavior is not discussed. The withdrawal of the Non-cooperation gives us the side of Gandhi as a whimsical leader; the explanation. The instinct in the Indian master narrative is to present secularism as an innate value of Indian nationalist movement. This allows the Indian writers to present demand for Pakistan later as sudden and ahistorical an act of manoeuvre on the part of Jinnah and the British, which is seen as a part of the ‘Divide and Rule’ policy of the British empire.
After the mid 1920s after the withdrawal of the Khilafat movement the writers with difficult years to dwell on. For the Indian narrative there are no dramatic events in this period. There was a lot of communal violence that took place during this period, which is ignored by both the sides. As the Pakistani narrative dwells on the characterization of the people on religious lines viz. Hindus and Muslims, the Indian narrative calls for characterization in terms of ‘nationalist’ and ‘communalist’. The young are trained to regard ‘nationalism’ and ‘communalism’ as antonyms.Nationalist as ones who fought on behalf of all Indians; communalist as one who fought for their own communities.
Why is this done? Why is the violence sidelined in both the narratives? One of the basic argument given in this favor of is that children should not be exposed to violence. But is this a valid argument? The reason for not exposing the children perhaps lies in the nature of nation building role which schools and history textbooks are supposed to perform. This role demands filtering out of the record of communal violence from the narrative of the national movement to whatever extent possible. Why should be this so?
In the Pakistani texts a key difference that is evident is in the portrayal of Congress. Congress is portrayed as a single, cohesive, Hindu body, without any internal differences. The Hindu Mahasabha, which was the right wing political party of the Hindus is politically and ideologically merged with the Congress. This is done so that a Hindu Congress can be well targeted in the Pakistani master narrative.
The Nehru Report
The report prepared by Motilal Nehru, known as the Nehru report is passingly mentioned in the Indian textbooks. But this report is one of the milestones in the history of Pakistan. From what is found that in the earlier episodes of history there is a difference of perspectives and approach in the two master narratives, but in this case there is a total disagreement. This is seen as the last straw of Congress-Muslim relationship. Jinnah presented his fourteen point program in response to this report. Whereas this response by Jinnah is hailed by Pakistani texts, as a step towards the reality of a Muslim nation, in the Indian texts this response is seen as ‘communal’ in character. In fact in the Indian texts there is a tacit policy to give no significance to organized Muslim response at the secondary level. To regard such demands as purely communal in nature, and to hold such ‘communal’ demands in sharp contrast to ‘national’ demands is to equal to thinking ahistorically. Then in such a framework of ‘communal’ and ‘national’ where does the support that Khilafat movement got [which was purely religious] fit in? Clearly the Indian textbook writers are missing the point here. How can one movement be ‘communal’ and the other be ‘national’? This clearly shows it as attempt to evaluate a given event with variable standards so as to ‘fit’ the master narrative.
After the 1930s the common points of reference between the two narratives become scarce, and they diverge rapidly. The two narratives employ different persons and events which lead to the desired end. The Indian narrative becomes vary fast in this case, whereas the Pakistani one becomes very slow detailing events that lead to the formation of Pakistani nation state. At this point how and why make the crucial difference between the orientations of the narratives. After the naming of Pakistan occurred, Pakistani account finds adequate reasons to under emphasize or altogether ignore even major events afterwards. On the other hand in the Indian narrative the task is to celebrate the struggle and the triumph of the ‘secular’ inspiration; due to this political struggle of religious and other separatists is forgotten. Even the mention of the names of important separatists like Subhas Bose are passingly mentioned.
Since the ‘communal’ activities increased in the last decade, Indian historians have to race through this decade. But in the Pakistani narrative this is the decade worth discussing. In this decade the Indian textbooks mainly concentrate on the civil disobedience movement. And the discussion usually starts with Gandhi’s Dandi march. But the issues and conditions under which this act was done remain mysterious. What exactly Gandhi hoped to achieve by this and why did he do it are unanswered questions. What is presented in the texts is just the factual information about the march without explaining the deeper meaning associated with it. Most of the Indian texts suppress the fact that civil disobedience did not attract the Muslim participation. Also worth noticing is the fact that reference to the Round Table Conferences and Poona Pact are meagre. The Indian historians looking at the events in the decade with a secular lens, fail to even mention the communal divide amongst the various sections in India. The reader is thus left unaware of the gravity of the communal problem present during this time. Still the image of all Indians, regardless of their religions, fighting against the British rule runs through the narrative. This creates an epistemic shock when demand for a separate Muslim state is made in the 1940s and the demand seems unjustified and ad hoc.
In Pakistani texts the three main things that, have a different focus than the Indian texts are.
- Focus on Iqbal’s Allahabad speech.
- Lack of emphasis on Civil Disobedience.
- Importance given to all three round table conferences.
And the key issue for the Pakistani texts remains the Congress’s refusal to acknowledge the minority problem. This struggle is presented in many texts as the struggle between the Father of Nation on the Indian side and Quaid-e-Azam on the other:
Gandhi insisted that there was only one nation India which were Hindus. But Quaid-e-Azam replied that Indian Muslims were also a separate nation of India which had its own interests.
Thus we see that the facts are once again presented in a way so as to fit the master narratives, leaving out the things that do not fit in, emphasizing only the aspects that do fit in the narrative.
The Government of India Act [1935]
Texts of both the countries mention the main provisions of this Act, in which regional governments were setup, in the different provinces, with the majority being in the hands of Congress. In the Indian texts little is said about the Congress being in power; the era presents no inspiring events for the reader. In the Pakistani texts the results of the election are portrayed as a shock to the League, and which saw a gloomy future for the Muslims if a democracy is setup in India. The Muslims due to smaller numbers will have no say in the government so formed democratically. This brought the Muslim league to the ground reality, also led the transformation of Jinnah from idealist to political realist.
During this era the Congress governments did some works, which is very sketchily or not mentioned at all. One of the works that Congress governments introduced was the Gandhi’s Wardha scheme for educational reforms. This is not mentioned or elaborated in the Indian texts. But contrastingly in the Pakistani texts this is one of key issues to be discussed. But why should just some educational reforms, that too at the school level should be worth discussing, when other major events are not discussed?
One of the key features of the Gandhi’s Wardha Scheme was the use of child’s mother tongue as a medim of instruction. Particularly in the United Provinces this meant that the traditional education in urdu to be replaced by that one in hindi. This scheme was seen as an alternative to bookish education. But in the implementation of the scheme many things happened which no body anticipated. The song of vande mataram was supposed to be sung by all school children, which is considered as anti-muslim in nature. Also in every school portraits of Gandhi were placed, which further made muslims irate. And finally the school were to be called vidya mandirs which means a temple of education, but this was very provocative for the muslims. The Muslims saw this scheme as a means to destroy their religion, by aiming at their children. Thus if the children are targeted and taken away from Islam, there would be no next generation of Muslims left in the country. This was a grand plot eliminate muslims forever. The interesting point to be noted is that, Gandhi had deliberately left out religious instructions in this scheme. But the things went the other way.
The contrast between the two texts sharpens as we enter the last phase of the struggle. Quit India movement is the major event in the early 1940s in the Indian narrative, whereas Lahore resolution is the major event in the Pakistani master narrative. The Quit India movement gives the Indian school historian a perfect material to dwell upon and write about in the master narrative. All the key elements of the narrative are present: adventure, heroism, moral struggle and determination. The movement is portrayed as the ultimate patriotic adventure with no trace of politics. The INA follows the Quit India and maybe seen as a continuation of the same. The differences between Subhas Bose and Gandhi are not highlighted. In case of the Pakistani master narrative Lahore resolution is the master narrative, whereas Quit India presented as detached, uninspiring story. The Muslim League is shown to have attained clarity and cohesiveness due to its bitter experience with Congress. The fact that League would push for independence not only from the British but also from Hindus, is seen as unavoidable. The Pakistani authors appear to be gripped at this juncture by the urge to trace and retrace the familiar record of past references to Hindu-Muslim differences and the idea of partition. The names like Lajpat Rai and Savarkar appear along with Syed Ahmad Khan and Iqbal in context of the idea of partition. Here the Congress is represented as a cohesive Hindu body aimed at destroying the Muslims.
The Cabinet Mission is mentioned, which was supposed to but what it meant or why it failed is hardly explained. The Congress-League relations in this era are not emphasized, while the Cabinet Mission plan is trivialized. In the Indian texts the structuring is around the anxiety to explain why the congress accepted partition. A feeling is created that partition was not completely inevitable but was allowed to take place. Now since the secular nationalism is a superior force, its proponents accepting proposal of division based on religious lines calls for an explanation. A distinction is made between the ‘acceptance’ of an impending course of events and the ‘acceptance’ of the inspiration that this impending course of events was based on. The second part consists of mitigating the scale of success which morally inferior idea of communalism achieved by forcing Partition. ‘The Nationalist leaders agreed to Partition of India in order to avoid the large scale blood bath that the communal riots threatened. But they did not accept the two nation theory.’ Thus Partition is seen as an outcome of circumstances, not as the failure of Congress’s ideology.
In the Pakistani narrative this is the peak of the narrative, the accomplishment of Partition is ascribed to Jinnah. Jinnah is portrayed as semi-divine visionary who succeeded against all odds in getting what he wanted. But the irony about the portrayal of the freedom struggle is that instead of its portrayal as inevitable destiny, it is a product of political happenings. The Muslim League is ascribed the intention of not letting the Congress gets it way, despite the backing of British. Thus we find in both the narratives the British being targeted as being the conspirators with the ‘other.’ A deep mistrust of the ‘other’ along with the British is present in both the narratives.
Here again one finds that the violence and the human tragedies that followed after the partition is not elaborated at all. It does not find more than a few lines in both the master narratives. As with the violence of 1857 the violence and bloodshed is underplayed. There can be three reasons which can be said about why violence is so under represented in both the texts.
- Partition is merely one of the topics that has to be covered.
- Sanitization of the freedom struggle.
- History as presently conceptualized, is incapable of dealing with the violence and suffering.
Some Reflections
We see that the histories of India and Pakistan as represented in their school textbooks have a relation that is far away from simple. The two narratives are related in a complicated way, to understand which it is hard for us as members of the Indian sub-continent to come above and see. It would be very hard for people like us to realize that the history that has been presented to us is ‘biased’ in a way so as to fit the ‘accepted’ or the state approved version of the history. But to have this realization is hard and once you have it it is still harder to let it go. You then tend to ‘see’ every thing with suspicion, with a feeling that you are being indoctrinated into something by someone who is invisible. Then the conspiracy theories are abound. But this realization must come from within, it is hard to come from without.

As for the Indian and Pakistani narratives, I have found a nice analogy which fits both the narratives. If we visualize the path from 1857 to 1945 as a path leading to a mountain summit, we can easily accommodate both of the master narratives nicely. Thus we have the events of 1857 as the starting point from where both the narratives diverge, the paths of the summit are different. Towards the summit the paths take different turns and different events happen in each of the expedition. Some of these events are seen by the people who have taken the ‘other’ path some of them are not. So in a log of the two expeditions which are our master narratives the politics of mention is thus taken into account. Each expedition encounters in their route something that the ‘other’ does not. As for the final summit, when they reach there in 1947, the members of the expedition look past each other and they are looking in different directions as, we see the idea of freedom is different in both the countries. Partition signifies end of history in India; in Pakistan it signifies birth.

Reference:
Krishna Kumar
Prejudice and Pride
2003, Penguin
PS: For a very dramatic account of the events leading to the freedom of India and Pakistan, and the violence that followed afterwards I would recommend
Freedom at Midnight by Larry Collins and Dominique Lapierre. Also for the events of 1857, fictional but highly readable account is Manohar Malgaonkar’s The Devil’s Wind.