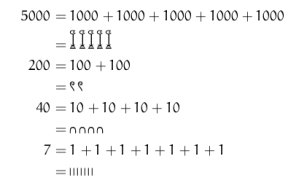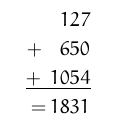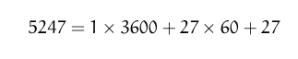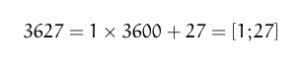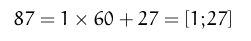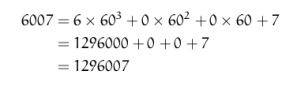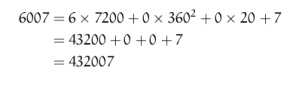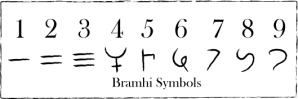For a proper understanding of the evolution and the need for the concept of zero we need to understand how our current number system has evolved from its ancestors. The very need for the concept of zero did not arise till the number systems themselves were well developed. The advancement in the number system necessitated the need for the concept of zero as we now know it. We can identify two distinct manifestations of zero; one is zero as a placeholder and the other is zero as a number, the former has much earlier origin than the later.
Humans probably before having the concept of numbers or counting then, would have begun with enumeration. By enumeration it is meant that we simply keep a track of objects in a collection or a set by matching the objects with other objects used as counters. A shepherd can keep the track of sheeps in the flock, by keeping pebbles which are equal in number to the number of sheep s in the flock or equivalently [if possible] by counting body parts. Then just by matching each sheep with each pebble the record of number of sheep s can be maintained. When the number of sheep s is increased or decreased the same number of pebbles or other counters can be increased or decreased correspondingly. The other counters that one can have for this type of counting can include the human body itself. In fact many primitive societies do indeed have a counting system based on the body parts. This is the most basic system of counting that we can have. No language is needed for such one-to-one counting.
When the languages developed, particular words were created for various body parts, so these words were used instead of the body parts themselves. This is a transition from enumeration to numeration. Thus one has to remember only the word names in order for counting. But this does not imply the idea of cardinality of number being present in this numeration. For the notion of cardinality of a number to be used in the idea of numeration it required some time. When the questions were asked in the form How many…? in the ancient texts, the answers to these type of questions are given best in terms of the cardinal number. From this further growth would be, the concept of ordinality i.e. the order of things is not important when counting objects. It relates to the fact that the last number enounced in a set not only assigns a certain name to the last object in the set to be matched but also tells us how many objects are there in that set altogether.
The further development of this numeration is the formation of numeration systems. The need for the number systems typically arose from the following question:
What is to be done when the finite ordered sequence of counters is exhausted, yet more objects remain to be matched?
This particular question was answered in different ways only one of which led us to the current number system we have. One of the most simple solutions to this is to extend the ordered sequence of counters. So that we invent new symbols or names to accommodate the excess objects that are to be matched. But this approach makes no sense when we have large number of objects that are to be matched.
A simpler way which lends itself well to the written representation, was extension by repetition. The extension by repetition implies a number system which is based on the additive principle. Most of the primitive number systems are based on the additive principle. Here the figures are entirely free. Their juxtaposition entails adding together their values. In a number system based on the additive principle it makes no difference where you place the symbols corresponding to the numbers. Some of the numbers systems based on the additive principle are; Egyptian, Cretan, Hittite, Greek, Aztec, Roman, Sumerian etc. As an example of the additive principle we consider the Egyptian system. In this system if we want to represent the number 5247 it can be represented in following ways:
When we break down the representation based on the additive principle we get the following:
Thus we see that in the representation of a number in the number systems based on the additive principle. Since addition is both commutative and associative, irrespective of where we place the base numbers the final number that is represented by the various combinations of these numbers remains the same.
This system though seems simple puts a lot of cognitive load on the user. First of all there are different symbols for different numbers and in many of these number systems the symbols have some intuitive association [at least in the lower range] to the number that they represent. So to represent large numbers a large number of different symbols were to be used. In our example of representing the number 5247 in the Egyptian hieroglyphic notation we have used a total of 18 symbols. Many times for representing large numbers new symbols had to be introduced. The arithmetic operations with these systems presented another difficulty. The number systems based on the additive principle are not well suited for arithmetic operations. For example consider the following sum in the Roman notation:
The above sum gives us no clue to what is supposed to be done. Though there are methods to perform this operations, but the procedures involved are very complicated. The above sum in the current notation would be:
In the number systems based on the additive principle the number signs are static in nature, which have no operational significance. The number signs in this case are more like abbreviations which can be used to write down the results of the calculations performed by some other means. To do arithmetical calculations, the ancients generally used auxiliary aids such as abacus or a table with counters.
The enumeration, numeration as we have seen do not have any requirement for the concept of zero as a numbe
r or a placeholder. The same is true with the number systems based on the principle of addition, in these systems there is no requirement of the concept of zero.
r or a placeholder. The same is true with the number systems based on the principle of addition, in these systems there is no requirement of the concept of zero.
The next step in the evolution of the number systems was the hybrid system, called so because it involves use of both addition and multiplication. In the hybrid system when the symbols for lets say symbols for 1000 and 5 are presented together, they meant 5 x 1000 = 5000, whereas in the additive system they will mean 1000+5=1005. In the hybrid system there were basic symbols for the numbers, and symbols for various powers of the base, for example in a base 10, system the symbols for 100, 1000 etc. These number systems used the additive principle for representing numbers below 100.
In case of complete hybrid systems there were special symbols for the numbers 1 – 9, and all numbers including the tens were represented as a product of these base numbers and the powers of 10. This increased the range of numbers that can be represented. The notable hybrid systems are Assyro-Babylonian, Phoenician, Singhalese, Mari, Chinese, Ethiopian, Tamil, Malayalam, and the Mayan. We consider an example from the complete hybrid systems to represent the number 5247 from \cite{uni1}.
When we break down the representation based on the multiplicative principle we get the following:
The hybrid systems thus need a specification of the powers of the base which, determine the value of the number in a given position. This brings us a step closer to the positional number systems based on the multiplicative principle. The hybrid system are not all forgotten and are still in use today. When we verbally read a number it is more of a hybrid number system that we use that a positional number system. That is to say when we read the number 5247, we spell it out as five-thousand two-hundred and forty-seven. Here when we verbally read a number we also explicitly give its corresponding powers just like in case of the hybrid number system. Even in this case the need for zero is not there, the hybrid systems can work without the use of the concept of zero.
So to conclude the hybrid systems are “Systems based [at least after a certain order] on a mixed principle [both additive and multiplicative] that invokes multiplication rule to represent consecutive order of units.”
We now move to the positional systems or multiplication based systems. These systems have a more abstract representation. The value of a figure in these positional systems varies according to the position in which it occurs in the representation of the number. Due to this the coefficients of the power of the base, into which the number has been decomposed appear. For example in a particular representation the actual value of a number, lets say 5 will depend on which position 5 is present in. If 5 is present in the units place then it represents 5, when it is present in the tens place it represents 50, and so on. If in the hybrid system if we remove the symbols used and just have the numbers only we have a positional number system. In this case the powers of the base for our case take base as 10, are implicitly figured out from the position of the numerals in the representation of the number. We know that in the positional representation of the number 5247, 5 is in the thousands place, 2 is in the hundreds place etc. Once this order is fixed then can we represent a number without any ambiguity? If we just consider the coefficients of the number 5247, the the answer to this probably seems to be true. But is it always so? For answer to this consider another example. Suppose we want to represent a number 1043 in the positional number system. In case of hybrid number system the representation would be like this:
so if we now drop the powers of the base, and just take the coefficients we are left with:
But this is not correct, since 143 is another number and not 1043.Similarly if we take just the coefficients of the number 10403, they are again 143. In case of the non-positional system this was not a problem, since every power and the corresponding coefficient was made explicit. But here if we just consider the coefficients of the number in a particular base, we cannot be sure that the number that we are representing is correct, unless we know for sure that a particular coefficient corresponding to a particular power is not present. In case of 1043 we have the coefficient of 100 absent. Some of the earliest positional systems that were developed suffered from the same problem. In case of the Babylonian system, we are not sure of how to read a particular number in many clay tablets, and the number has to be guessed from the context of the problem. Since the Babylonians used a base of 60, so a number [lets take 5247] was represented as:
In this case there was no ambiguity in base 60 number would be written as [1;27;27]. But even in this case there was no guarantee that the number represented is the number that we want. Suppose if we want to represent 3627 in this notation, then it would be represented as:
Thus we see that in case of the positional number system we required a notion that tell us whether a particular coefficient is absent. This requirement initiated the need for the concept of zero. So the discovery of zero was therefore a necessity for the strict and regular use of the rule of the position, and it was therefore a decisive stage in the development of mathematics. So how do we make sure that something is not present in a particular position in a given positional representation of a number. It becomes essential then to have a special sign whose purpose is to indicate the absence of anything in particular position. This thing which signifies nothing, or the empty space, is in fact the \textsl{zero}. As \cite{uni1} pg. 668 puts it: “To arrive at the realisation that empty space may and must be replaced by a sign whose purpose is precisely to indicate that it is empty space: this is the ultimate abstraction, which required much time, much imagination, and beyond doubt great maturity of mind.”
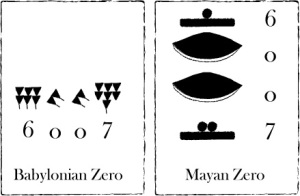
The concept of zero has been discovered three times in the history independently. It was discovered first by the Babylonians, the Mayans and the Indians. All these three civilizations used the positional number system for which the concept of zero is needed. The Babylonians tried to get away with this difficulty by l
eaving empty space where the missing coefficients of particular order were to be found. Hence they would write a number such as [1; 6] for lets say 3606. But this did not solve the problem completely. In copy or reading these spaces could be overlooked, and particularly when two or more space were to be given it could be confused with one space. But since the Babylonians has the base as 6o the need for writing numbers with zero in between arises on a very few occasions than it does in the number system with base 10. In case of the sexagesimal numeration only in 59 integers below 3600 this arises; as compared to 917 cease in the base 10 system \cite{boyer}. The Babylonian zero is the first zero to arrive on the scene. To denote absence of a coefficient of a particular order in their representation of the number, the Babylonians used a special sign [after fourth century BCE], which is the a cuneiform sign looking like a double oblique chevron. The Mayans developed their positional system with base 20, but they were not consistent with the use of the powers of the base after the third position \cite{uni2} pg 670. The Mayans understood the concept of zero sign, but they did not have its operational usability due to their inconsistent positional system. In case of the Babylonians it was never understood as a number synonymous with empty and never corresponded to the meaning of null quantity. So we see that in spite of having the notion of zero the Mayans and teh Babylonians did not get much further in this. The Mayan and the Babylonian zeros are as given in the figure.
eaving empty space where the missing coefficients of particular order were to be found. Hence they would write a number such as [1; 6] for lets say 3606. But this did not solve the problem completely. In copy or reading these spaces could be overlooked, and particularly when two or more space were to be given it could be confused with one space. But since the Babylonians has the base as 6o the need for writing numbers with zero in between arises on a very few occasions than it does in the number system with base 10. In case of the sexagesimal numeration only in 59 integers below 3600 this arises; as compared to 917 cease in the base 10 system \cite{boyer}. The Babylonian zero is the first zero to arrive on the scene. To denote absence of a coefficient of a particular order in their representation of the number, the Babylonians used a special sign [after fourth century BCE], which is the a cuneiform sign looking like a double oblique chevron. The Mayans developed their positional system with base 20, but they were not consistent with the use of the powers of the base after the third position \cite{uni2} pg 670. The Mayans understood the concept of zero sign, but they did not have its operational usability due to their inconsistent positional system. In case of the Babylonians it was never understood as a number synonymous with empty and never corresponded to the meaning of null quantity. So we see that in spite of having the notion of zero the Mayans and teh Babylonians did not get much further in this. The Mayan and the Babylonian zeros are as given in the figure.
If we work out the number represented in these notation the numbers are:
In the Babylonian notation.
In the Mayan notation.
The credit of having a well conceived positional system, which is operationally useful goes to the Indians. This step was taken by simplifying the hybrid notation, by suppressing the signs indicating the powers of the base. This required a much higher level of abstraction: the zero. This can be regarded as “… the supreme discovery of mathematicians who soon would come to extent it, form its first role of representing empty space, to embrace truly numeric meaning of a null quantity.” The Indian civilization was the only one to achieve this great feat. This system came up as a result of conjunction of three great ideas :
1.The idea of attaching each basic figure with signs removed from intuitive associations.2. The idea of a positional number system, in which the value of a number depends on its position in the representation.3. The idea of a full operational zero, filling the empty spaces of missing units and at the same time having the meaning of a null number.
In the system thus developed it does not matter what signs or base we use for the system, if it rests strictly and rigorously of the principle of position and incorporates the full concept of the symbol for zero. The discovery of zero in India and the place value were inventions unique to the Indian civilization. The roots of the development of the positional number system in India can be traced to the use of spoken sanskrit [संस्कुत] numeral system [Treatment of the development of Indian positional system follows from \cite{uni1}, \cite{uni2}]. The sanskrit spoken language has for each power of ten an individual name, “… so that to express a given number, one only had to place the name indicating the order of units between the name of the order of units that was immediately below it and immediately above it.” In fact there are names to the powers of 10 till 10^140 \cite{uni2} pg. 134. This is what is required in a positional number system. From the sanskrit spoken numeral system the Indian system of numerical symbols was formed. As soon as place value system was rigorously applied to the nine simple units, the use of a special terminology was indispensable to indicate the absence of units of a particular order. The sanskrit language already possessed the word shunya [शुन्य] to express void or absence, which also an element of mystical and religious philosophy. So to express the new mathematical notion of zero the term shunya could be used. This is how the word came to perform the function of zero as a part of the counting system.
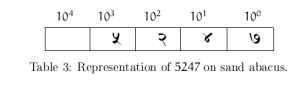
Indian mathematicians before discovering the place value system, used their fingers or concrete mathematical devices. The most common was the abacus; from left to right, the columns representing the various powers of ten. The first nine numerals were traced in sand or dust, inside the column of a particular decimal order. Thus the number 5247 would have been represented in the following manner :
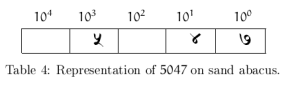
If a particular order of units was missing, one only needed to leave that particular column empty. Thus for representing 5047 we would write:
So with all this the necessary ‘ingredients’ for the creation of the written place value system had been amassed by the Indians:
- Distinct representation of one to nine numbers, which had forms unrelated to the number they represented.
- Discovery of the place value system.
- Invention of the concept of zero.
Still some things were still absent for the perfection of the number system:
- The nine numerals were only used in accordance to addition principle for analytical combinations using numerals higher than or equal to ten, the notation was very basic and limited to numbers below 100,000.
- Place value system was only used with sanskrit names for numbers.
- Zero was only used orally.
The only thing that remained was to combine these ideas. By using the nine bramhi [ब्राम्ही] numerals on the dust abacus this stage already had been reached.
The two methods of expressing the numbers bramhi numerals and sanskrit names of numbers were known to the Indian mathematicians. In the dust abacus the numbers were drawn in contemporary style. The numbers in sanskrit were expressed in orders of ascending powers of ten; from the smallest to the highest. So that 4769 is written as:
And it is read in sanskrit as:
नव शष्टि सप्तशत् च चतुरसहस्त्र
Meaning: nine sixty seven hundred and four thousand.
In the written numerals however the opposite order was used. The evidence for these methods goes back to third century BCE. IF we look at these two opposite ways of representing the number, indicates an inconsistency. This is what the Indian mathematicians expressed as :
अंकानाम वामतो गति:
Meaning: principle of the movement of numerals from the right to the left.
Since the brahmi had a limited numeral base [highest number expressed was 90,000], so any calculation larger than this was to be expressed in the sanskrit names for the numbers. In the dust abacus extremely large computations could be performed, and the successive columns in the abacus always rigorously corresponded to the consecutive powers of ten. The same mathematical structure was present in the sanskrit counting system. Thus each system was a mirror image of the other. Though the numbers are read from the right to the left from the smallest to the largest. The structure of the abacus is such that the mathematician has no other choice but to follow the principle
अंकानाम वामतो गति: principle of the movement of numerals from the right to the left.
The solution to write a number in this way was to start with the column for the simple units. This led to the abandonment of the old system. By beginning with highest power of ten, one immediately knows the size of number we are dealing with, but this did not facilitate drawing. Hence the opposite system was adopted; no matter how high a number, there could be no mistake as to which column to write it in. This was conserved when the positional notation was invented using numerical symbols.
All this lead to the following notation, “the numbers reading from left to right in descending powers of ten, constituting a faithful reproduction, minus the columns, of its representations on the abacus, as well as reflection of the abridged form of the corresponding sanskrit expression. Thus came the decimal position values which were given to the first nine numerals of the old notation. This was the birth of the modern numerals.
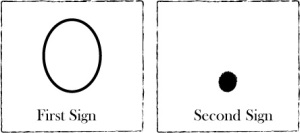
Now to convey the absence of units in a particular decimal order a new symbol was necessary. This was not required in the case of the abacus, but in the new positional system it became a necessity. The language already had the word symbol that expressed the concept zero, the shunya, it also conveyed the concepts such as sky, space etc. The circle has been considered as the representation of the sky, hence through a simple transposition of ideas it came to represent the concept of zero. Another sanskrit term representing zero was bindu [बिंदु], which literally means “point”. The point is the most insignificant geometrical figure, but for Indians the point represents the universe in non-manifest form. The point is the elementary of all geometrical figures, with potential for creating all the shapes, and hence was associated with zero. Zero is the most negligible quantities, but most fundamental of all abstract mathematics. The point also thus came to represent the zero. The two forms of the Indian zero are as shown in the figure below.The most likely time that the positional value system and zero were discovered is in the middle reign of the Gupta dynasty which ruled the Gangetic plains from about 240 to about 535 CE.
Along with the loaded philosophical connotations that were associated with the word shunya it served to mark the absence of units within a given decimal order in any position; the point or the little circle were used in the same way. This zero was also a mathematical operator; if placed after a number, it meant the number was multiplied by ten. Thus the three significant ideas that we have mentioned earlier were combined to give us the modern positional number system. Soon after this the concept of zero was perfected. Zero was given the status of a number, i.e. to say its cardinality was recognised. After this various arithmetic operations on and with zero were defined, which led to foundation of modern algebra .
The Arabs got this positional number systems from the Indians. The Europeans in turn got this system from the Arabs. The origin of the word zero or cipher can be traced back to this transfer of the positional number system to the Europeans from the Arabs. The Indian word for zero is shunya, from this the Arabic name sifr meaning vacant was given. When this was transferred to the Europeans the sound was kept but not the sense; Fibonacci called it zephirum. This was then passed over as zeuro, ceuero, and zepiro, which finally led to the current day synonyms which are the zero and the cipher.
References
Boyer C. B. :
Zero: The Symbol, the Concept, the Number
National Mathematics Magazine, Vol. 18, No. 8 , May 1944
Irfah G. :
The Universal History of Numbers I
Penguin, 2005
Irfah G. :
The Universal History of Numbers II
Penguin, 2005
Ore O. :
Number Theory and Its History
Dover, 1948