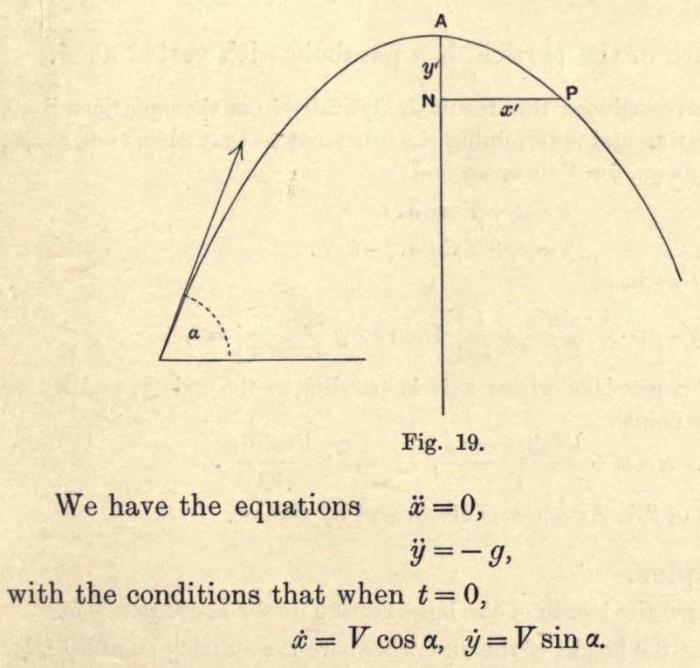huxley

The Mitr

Algorithmic Nature

Such natural beauty! Does mathematics lie at the basis of these diverse and beautiful forms? Photo taken during summer of 2017 in Mumbai. None of these are native to India. On left: The Cannonball tree flower (Couroupita guianensis) is South and Central American, African Tulip Tree (Spathodea campanulata) native to tropical. Africa; On Right: The Cannonball tree flower, and Gulmohar is Madagascan (Delonix regia).

What could be more “organic” and “natural” than looking at a pristine forest with a variety of tree forms and leaf forms of various shapes and shades, with inflorescences of variety of shapes, sizes and colours? Mathematicians and physicists are often accused of being not able to enjoy nature and because mathematics and physical theory is so “abstract” and nature is so “organic”. Organic growth is in the form of variety of morphologies of roots, branches, flowers shapes and arrangement, leaf shapes and arrangements, while mathematics typically is abstract graphs, equations, symbols and numbers. How can these two possibly have anything in common? This has also to do with how biology is traditionally taught. While physics has mathematics at its foundation, the teaching of biology doesn’t acknowledge any need for mathematics – it is mostly descriptive as it was in its early stages a couple of centuries later. This is more so at the school level teaching of biology. So this creates an impression in the students and teachers alike that mathematics is not a part of “biological” nature and it is only reserved for falling bodies and ascending projectiles. 

 

What can be similarities in the two images? One is abstracted representation of motion of a body in algebraic and graphical format and other is organic growth of a plant showing its branching and similar leaves with its pigmentation of chlorophyll.

Of course the variety of forms and their classification is one of the foundations of biology. Linnaeus used the morphological differences and similarities to form his classification system.

 

Linnaean system brought order to seemingly diverse and chaotic forms of natural world. Linnaeus named the different forms. Naming is the first step in studying anything. Naming helps in categorisation, which is one of ways to formation of concepts. This led to further finer classification of the system as whole which now includes both flora and fauna. Then began the programme of finding organisms and classifying them in existing categories with descriptions – or creating new ones when the existing ones did not fit – became the normal way of doing biology in the nineteenth century. Even now finding a new plant or animal species is treated with celebrated as a new discovery. 

Darwin in his thesis about evolution by natural selection used the differences and similarities of the form as one of evidence. He theorised that organisms that have evolved from common ancestors will show similar forms with slight variations. Over long periods of time these slight variations evolve into larger variations which ultimately leads to a completely different species. Fossil records tell us about ancestors and current relatives of organisms.

There is grandeur in this view of life, with its several powers, having been originally breathed by the Creator into a few forms or into one; and that, whilst this planet has gone circling on according to the fixed law of gravity, from so simple a beginning endless forms most beautiful and most wonderful have been, and are being evolved. (emphasis added)

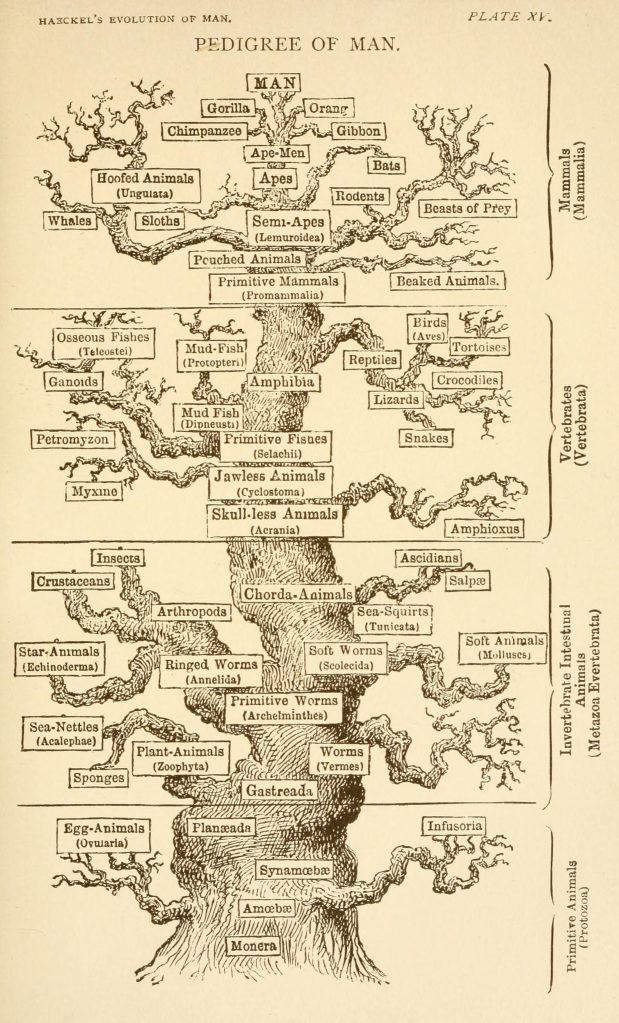
The morphologies tell us about related species, the ancestries and divergences from there. The fossils tell us the ancestors, the missing links. So finding organisms, both extant and extinct, to fit in the jigsaw puzzle of tree of life became the standard programme in biology. This enabled us to construct the tree of life. Ernst Haeckel’s version of the tree, depicted below, is highly anthropocentric which places humans at the apex of evolution. This is rather common misconception about evolution – humans are not at apex of evolution or the prime product of it as some would have us believe – we have co-evolved with all the current extant species. Evolution by natural selection is not anthropocentric, it is indifferent to humans and other organisms alike. Daniel Dennett likens it to universal acid, and makes a point that it is not only applicable to living systems, but applies to any system which fulfil the three required criteria. 

 

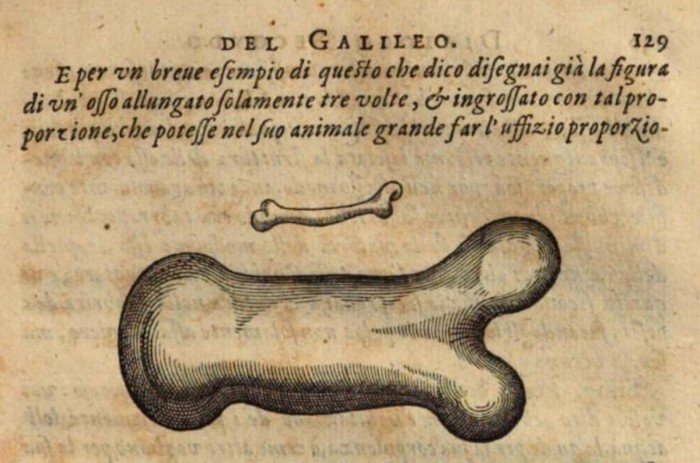
Haeckel’s – Pedigree of Man – a version of tree of life which is highly anthropocentric.

But can we make sense of similarities of the form in terms of mathematics? Can we find mathematical algorithms which will generate forms, as they generate trajectories of moving projectiles? Looking at similarities in form, it is Galileo who was one of the first to discuss the problem of scaling and its effect on form.

To illustrate briefly, I have sketched a bone whose natural length has been increased three times and whose thickness has been multiplied until, for a correspondingly large animals, it would perform the same function which the small bone performs for its small animal, From the figures here shown you can see how the proportion of the enlarged bone appears. 

…

Whereas, if the size of a body be diminished, the strength of that body id not diminished in the same proportion; indeed the smaller the body the greater its relative strength. Thus a small dog could probably carry on his back two or three dogs of his own size; but I believe that a horse could not carry even one of his own size.

At the start of twentieth century we had a few  classics which gave a strong mathematical flavour to the study of the biological forms and scaling – The Curves of Life by Theodore Cook (1914), D’arcy Thompson’s  On Growth and Form (1917) and  Julian Huxley’s Problems of Relative Growth (1932). 

The kind of mathematical treatment that entered in study of biology by above classics looked at the mathematical aspects of morphological forms in organisms. The Curves of Life looks at the spiral forms which are found in nature, and also in various human creations – architecture and art. 

The spiral is one of the most easily identifiable mathematical forms in nature.
In many flowers, a double spiral forms the basis of the central pattern. The Fibonacci numbers are easily identifiable with this pattern.
The spiral is found in animals too, most easily identifiable in the shells of various types. They represent logarithmic spirals.

 

Despite tremendous success of Darwin’s theory, physics and mathematics were in a separate compartment from biology. There seemed to be no common elements, while biology became more and more descriptive with focus on the form, but not mathematical. 

The word “form” in this article will refer to the shapes of material objects, the arrangement in space of groups of them, and the arrangement in space of their component parts. Our appreciation of form is partly sensory, but we can be helped by measurement and calculation to gain some confidence that what we perceive is not entirely unconnected with the outside world. (Physical Principles underlying Inorganic Form – S.P.F. Humphreys-Owen)

But this is a folly. Nature and organic growth is as mathematical as is the description of a projectile flying under gravity. Perhaps the mathematical description is 

The sparse branching of Frangipani (Plumeria sp.), a native of central America.
The dense branching of the Acacia (Vachellia nilotica) native to Africa, Middle East and India. Is the branching in Frangipani and Acacia related? What about the branching in grass in the figure at top? Can these be generated from a single mathematical algorithm? And why do only these forms are found and not any other?

In my experience a lot of young children who take to biology do so because they hate mathematics or computations. In India there are even streams at +2 level which allow you to shun mathematics for biological subjects. This utter hatred for mathematics is, IMHO, due to a carelessly designed and too abstracted mathematics curriculum at the school level – a curriculum which takes out the soul of mathematics and puts on a garish display of the cadaver of mathematics with bells and whistles. But this post is not about the problems of mathematics education, I have talked about it elsewhere.

 

The aim of this series of posts is to touch upon the inherent mathematics and algorithms in the natural world. How nature is mathematical especially in living and non-living things. How can algorithms generate natural forms? In the next posts in this series we will explore how the ideas of mathematical models can explain the variety of forms that result from natural selection in environment and possibly why only those forms can be found. 

Note: All photographs were taken by me over the years. Only now I am able to piece a narrative linking them together.

 

 

The Mitr

Conditioning hatred for books

INFANT NURSERIES. NEO-PAVLOVIAN CONDITIONING ROOMS, announced the notice board.
The Director opened a door. They were in a large bare room, very bright and sunny; for the whole of the southern wall was a single win-dow. Half a dozen nurses, trousered and jacketed in the regulation white viscose-linen uniform, their hair aseptically hidden under white caps, were engaged in setting out bowls of roses in a long row across the floor. Big bowls, packed tight with blossom. Thousands of petals, ripe-blown and silkily smooth, like the cheeks of innumerable little cherubs, but of cherubs, in that bright light, not exclusively pink and Aryan, but also luminously Chinese, also Mexican, also apoplectic with too much blowing of celestial trumpets, also pale as death, pale with the posthumous whiteness of marble.
The nurses stiffened to attention as the D.H.C. came in.
“Set out the books,” he said curtly.
In silence the nurses obeyed his command. Between the rose bowls the books were duly set out-a row of nursery quartos opened invitingly each at some gaily coloured image of beast or fish or bird.
“Now bring in the children.”
They hurried out of the room and returned in a minute or two, each
pushing a kind of tall dumb-waiter laden, on all its four wire-netted
shelves, with eight-month-old babies, all exactly alike (a Bokanovsky
Group, it was evident) and all (since their caste was Delta) dressed in
khaki.
“Put them down on the floor.” The infants were unloaded.
“Now turn them so that they can see the flowers and books.”
Turned, the babies at once fell silent, then began to crawl towards those clusters of sleek colours, those shapes so gay and brilliant on the white pages. As they approached, the sun came out of a momentary eclipse behind a cloud. The roses flamed up as though with a sudden passion from within; a new and profound significance seemed to suffuse the shining pages of the books. From the ranks of the crawling babies came little squeals of excitement, gurgles and twitterings of pleasure.
The Director rubbed his hands. “Excellent!” he said. “It might almost have been done on purpose.”
The swiftest crawlers were already at their goal. Small hands reached out uncertainly, touched, grasped, unpetaling the transfigured roses, crumpling the illuminated pages of the books. The Director waited until all were happily busy. Then, “Watch carefully,” he said. And, lifting his hand, he gave the signal.
The Head Nurse, who was standing by a switchboard at the other end of the room, pressed down a little lever.
There was a violent explosion. Shriller and ever shriller, a siren shrieked. Alarm bells maddeningly sounded.
The children started, screamed; their faces were distorted with terror.
“And now,” the Director shouted (for the noise was deafening), “now we proceed to rub in the lesson with a mild electric shock.”
He waved his hand again, and the Head Nurse pressed a second lever. The screaming of the babies suddenly changed its tone. There was something desperate, almost insane, about the sharp spasmodic yelps to which they now gave utterance. Their little bodies twitched and stiffened; their limbs moved jerkily as if to the tug of unseen wires.
“We can electrify that whole strip of floor,” bawled the Director in explanation. “But that’s enough,” he signalled to the nurse.
The explosions ceased, the bells stopped ringing, the shriek of the siren died down from tone to tone into silence. The stiffly twitching bodies relaxed, and what had become the sob and yelp of infant maniacs broadened out once more into a normal howl of ordinary terror.
“Offer them the flowers and the books again.”
The nurses obeyed; but at the approach of the roses, at the mere sight of those gaily-coloured images of pussy and cock-a-doodle-doo and baa-baa black sheep, the infants shrank away in horror, the volume of their howling suddenly increased.
“Observe,” said the Director triumphantly, “observe.”
Books and loud noises, flowers and electric shocks-already in the infant mind these couples were compromisingly linked; and after two hundred repetitions of the same or a similar lesson would be wedded indissolubly. What man has joined, nature is powerless to put asunder.
“They’ll grow up with what the psychologists used to call an ‘instinctive’ hatred of books and flowers. Reflexes unalterably conditioned. They’ll be safe from books and botany all their lives.” The Director turned to his nurses. “Take them away again.”
Aldous Huxley, Brave New World

Though fictionalised the above passages capture what makes people hate books in general. The conditioning happens in reality in a more subtle manner. The conditioning laboratory is the school. In school children are made to engage with the books, textbooks in most cases, in the most artificial and dishonest matter. Another problem is the quality of textbooks themselves. Though the school has a “textbook culture”, not enough effort is put in by the writers and designers of the textbooks to make the best that they can offer. Instead cheap, copy-paste techniques, and a mix-and-match fashioned content is crammed and printed onto those pages glued together called as textbooks. No wonder, people when they grow up don’t like books or run away at the sight of them. Its just behaviorism at work with Pavlov portrait in the background.