At times in LaTeX you want to introduce a small space between words. This is especially important in mathematical typesetting. Just adding a little bit of space hairspace, can alter the aesthetic look of the equation or mathematical entity substantially. For example consider this expression:
$|a|^{2}$
This produces the following

The | braces are too close to the character “a”. To create a better version of this we introduce a small hairspace between the two. The code for hairspace is \,.
$|\,a\,|^{2}$
This produces a much nicer looking expression.

This feature of hairspace was known to me for some time. But the problem came when I had to create a negative space. Take for example this expression:
$F_{eff} = kx$
The result of this is not so nice looking as you can see:
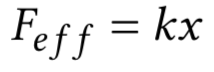
But then I came to know about a negative hairspace. The code for it is \!. Now let us introduce this in the above expression
$F_{e\!f\!\!f} = kx$
The result is much better visually:
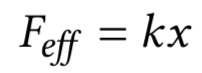
mathematical
Topological Art
ILLUSTRATIONS FOR TOPOLOGY
From the book Introduction to Topology by Yu. Borisovich, N. Bliznyakov, Ya. Izrailevich, T. Fomenko. The book was published by Mir Publishers in 1985.

ILLUSTRATION TO CHAPTER I
The central part of the picture presents the standard embedding chain of crystalline groups of the three dimensions of Euclidean space: their standard groups embedded into each other are depicted as fundamental domains (Platonic bodies: a cube, a tetrahedron, a dodecahedron). The platonic bodies are depicted classically, i.e., their canonical form is given, they are supported by two-dimensional surfaces (leaves), among which we discern the projective plane (cross-cap), and spheres with handles. The fantastic shapes and interlacings (as compared with the canonical objects) symbolizes the topological equivalence.
At the top, branch points of the Riemann surfaces of various multiplicities are depicted: on the right, those of the Riemann surfaces of the functions w=5z√ and w=z√; on the left below, that of the same function w=z√, and over it, a manifold with boundary realizing a bordism mod 3.

ILLUSTRATION TO CHAPTER II
The figure occupying most of the picture illustrates the construction of a topological space widely used in topology, i.e., a 2-adic solenoid possessing many interesting extremal properties. The following figures are depicted there: the first solid torus is shaded, the second is white, the third is shaded in dotted lines and the fourth is shaded doubly. To obtain the 2-adic solenoid , it is necessary to take an infinite sequence of nested solid tori, each of which encompasses previous twist along its parallel, and to form their intersection.
Inside the opening, a torus and a sphere with two handles are shown. The artist’s skill and his profound knowledge of geometry made it possible to represent complex interlacing of the four nested solid tori accurately.

ILLUSTRATION TO CHAPTER III
The canonical embedding of a surface of genus g into the three-dimensional Euclidean space is represented 0n the right . A homeomorphic embedding of the same surface is shown on the left . The two objects are homeomorphic, homotopic and even isotopic . The artist is a mathematician and he has chosen these two, very much different in their appearance, from an infinite set of homeomorphic images.

ILLUSTRATION TO CHAPTER IV
Here an infinite total space of covering over a two-dimensional surface, viz., a sphere with two handles, is depicted. The artist imparted the figure the shape of a python and made the base space of the covering look very intricate. Packing spheres into the three-dimensional Euclidean space and a figure homeomorphic to the torus are depicted outside the central object. The mathematical objects are placed so as to create a fantastic landscape.

ILLUSTRATION TO CHAPTER V
A regular immersion of the projective plane RP2 in R3 is represented in the centre on the black background. The largest figure is the Klein bottle (studied in topology as a non-orientable surface) cut in two (Moebius strips) along a generator by a plane depicted farther right along with the line intersection; the lower part is plunging downwards; the upper part is being deformed (by lifting the curve of intersection and building the surface up) into a surface with boundary S1; a disc is being glued to the last, which yields the surface RP2. The indicated immersion process can be also used for turning S2 `inside out’ into R3.
On the outskirts of the picture, a triangulation of a part of the Klein bottle surface is represented.
A detailed explanation of this picture may serve as a material for as much as a lecture in visual topology.

