misconceptions

The Mitr

What is the mathematical significance of the constant C in an indefinite integral?

As we had seen in an earlier post, calculus bottleneck, calculus presents one of the most difficult topics for the students in higher mathematics. But the problem is not just limited to the students. Teachers feel it too. Too often the emphasis is given on how to solve integration and differentiation problems using “rules” and “methods” while the essence of what is happening is lost. Recently, I asked this question in an interview to a mathematics teacher who was teaching indefinite integration. This teacher had almost a decade of experience in teaching mathematics at +2 level. The teacher tried to answer this question by using an example of the function \(x^{2} + 5 \). Now when we take the derivative of this function, we get

\[ \dv{  (x^{2} + 5)}{x} = \dv{x^{2}}{x} + \dv{5}{x} = 2x \]

as derivative of a constant (5 on our case) is 0). Now the teacher tried to argue, that integration is the reverse of the derivative), so

\[ \int 2x \, \dd x = \frac{2x^{2}}{2} + C = 2x + C \]

After this the teacher tried to argue this \( C \) represents the constant term (5) in our function \(x^{2} + 5 \). He tried to generalise the result, but he was thinking concretely in terms of the constant in the form of the numbers in the function. The teacher could understand the mechanism of solving the problem, but was not able to explain in clear mathematical terms, why the constant \( C \) was required in the output of the indefinite integral. This difficulty, I think, partly arose because the teacher only thought in terms solving integrals and derivatives in a particular way, and knew about the connection between the two, but not in a deep way. He did in a way understood the essence of the constant \( C \), but was not able to understand my question as a general question and hence replied only in terms of concrete functions. Even after repeated probing, the teacher could not get the essence of the question:

why do we add a constant term to the result of the indefinite integral?

To put it in another words, he was not able to generalise an abstract level of understanding from the examples that were discussed. The teacher was thinking only in terms of symbol manipulation rules which are sufficient for problem solving of these types. For example, look at the corresponding rules for differentiation and integration of the function \(x^{n} \).

\[ \dv{x^{n}}{x} = n x^{n-1}  \iff  \int x^{n} \dd x = \frac{x^{n+1}}{n} + C \]

Thus, we see according to above correspondence that adding any extra constant \( C \) to the derivative formula will not affect it. So the teacher claimed it is this constant which appears in the integration rule as well. In a way this is a sort of correct explanation, but it does not get to the mathematical gist of why it is so. What is the core mathematical idea that this constant \( C \) represents.

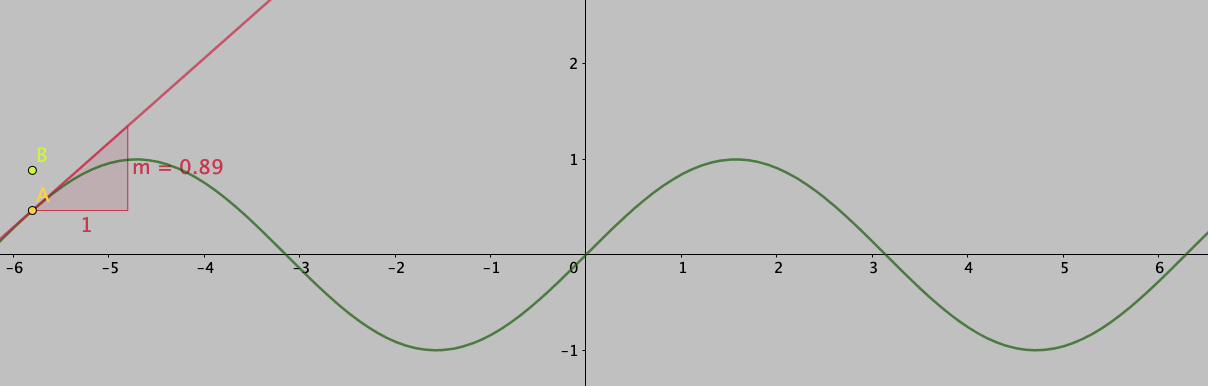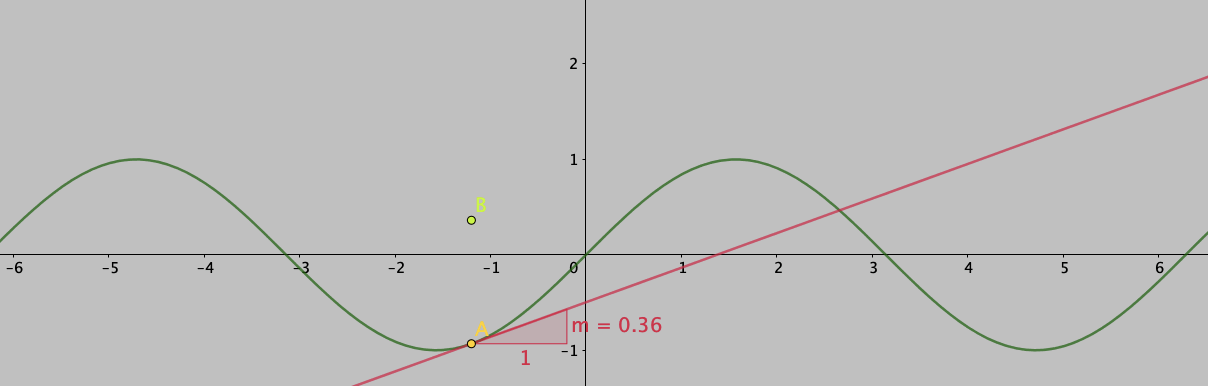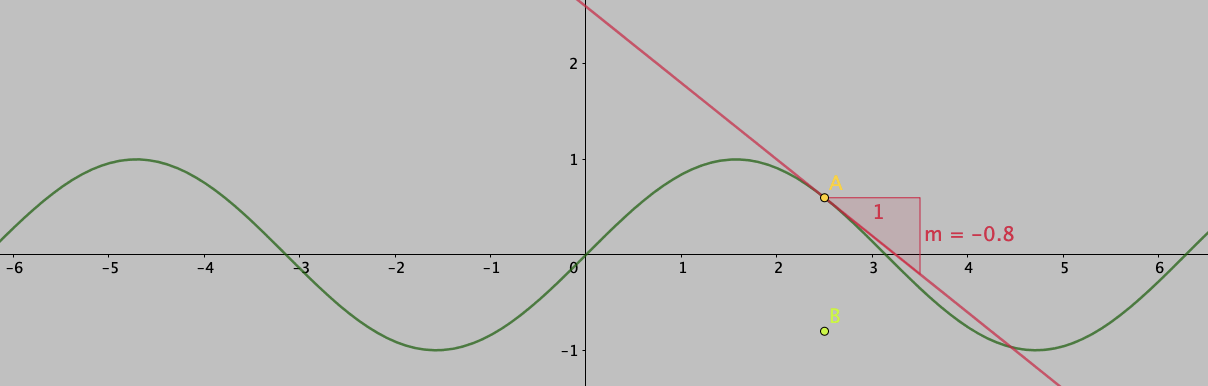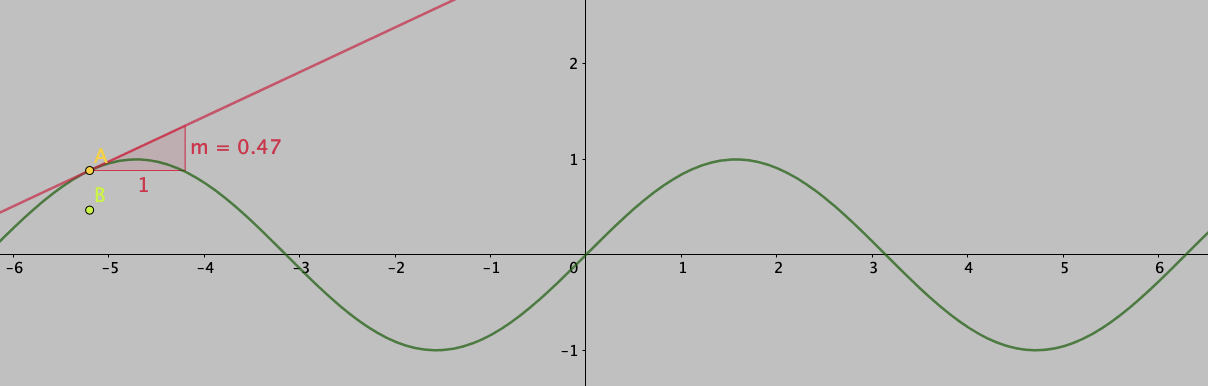
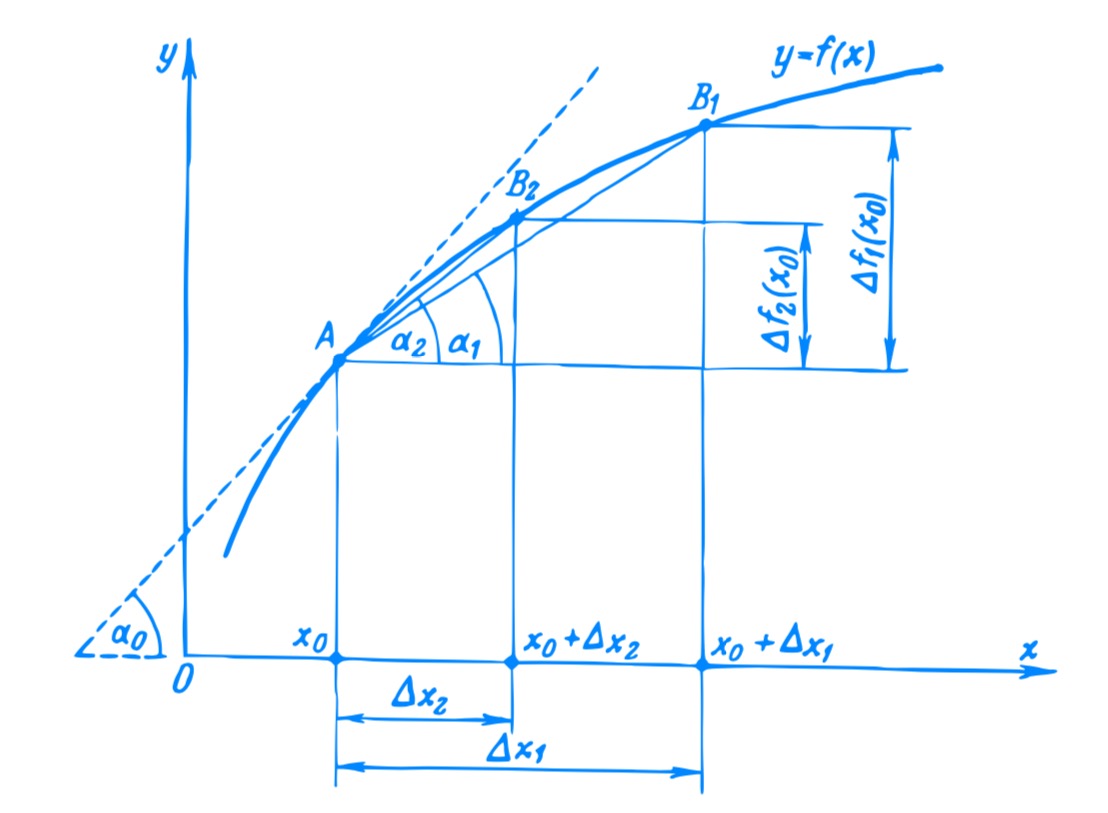
Another issue, I think, was the lack of any geometrical interpretation during the discussion. If you ask, what is the geometrical interpretation of the derivative you will get a generic answer along the lines: “It is the tangent to the curve” and for integration the generic answer is along the lines “It is the area under the curve”. Both these answers are correct, but how do these connect to the equivalence above? What is the relationship between the tangent to the curve and area under the curve which allows us to call the integral as the anti-derivative (or is the derivative an anti-integral?). I think to understand these concepts better we have to use the geometrical interpretation of the derivative and the integral from their first definitions.

The basic idea behind the derivative is that it represents the rate of change of a function \( f \) at a given point. This idea, for an arbitrary function, can be defined (or interpreted) geometrically as:

The derivative of a function \( f \) at a point \( x_{0} \) is defined by the slope of the tangent to the graph of the function \( f \) at the point  \(x =  x_{0} \).

The animation below shows how the slope of the tangent to the sine curve changes. Point \( B \) in the animation below plots the \( (x, m) \), where \( m \) is the slope of the tangent for the given value of \( x \). Can you mentally trace the locus of point \( B \)? What curve is it tracing?
Now, the tangent to any point on a curve is unique. (Why is it so?) That means if one evaluates a derivative of a function at a point, it will be a unique result for that point.
This being cleared, now let us turn to the indefinite integral. One approach to understanding integration is to consider it as an inverse operation to the derivative, i.e. an anti-derivative.

An anti-derivative is defined as a function \( F(x) \) whose derivative equals an initial function \(f (x) \):

\[ f(x)= \dv{ F(x)}{x} \]

Let us take an example of the function \( f(x) = 2x^{2} – 3x \). The differentiation of this function gives us its derivative \(f'(x) = 4x – 3 \), and its integration gives us anti-derivative.
\[ F(x) = \frac{2}{3} x^{3} – \frac{3}{2} x^2 \]

This anti-derivative can be obtained by applying the known rules of differentiation in the reverse order. We can verify that the differentiation of the anti-derivative leads us to the original function.

\[ F'(x) = \frac{2}{3} 3 x^{2} – \frac{3}{2} 2 x = 2x^{2} – 3x \]

Now if add a constant to the function \( F(x) \), lets say number 4, we get a function \( G(x) = \frac{2}{3} x^{3} – \frac{3}{2} x^2 + 4 \). If we take the derivative of this function \( G(x) \), we still get our original function back. This is due to the fact that the derivative of a constant is zero. Thus, there can be any arbitrary constant added to the function \( F(x) \) and it will still be the anti-derivative of the original function \( f(x) \).

An anti-derivative found for a given function is not unique. If \( F (x) \) is an anti-derivative (for a function \( f \) ), then any function \( F(x)+C \), where \( C \) is an arbitrary constant, is also an anti-derivative for the initial function because
\[
\dv{[F(x)+C]}{x} = \dv{ F(x)}{x} + \dv{ C}{x}= \dv{ F(x) }
\]

But what is the meaning of this constant \( C \)? This means, that each given function \( f (x) \) corresponds to a family of anti-derivatives, \( F (x) + C \). The result of adding a constant \( C \) to any function is that it shifts along the \( Y \)-axis.

Thus what it means for our case of result of the anti-derivative, the resultant would be a family of functions which are separated by \( C\). For example, let us look at the anti-derivative of \( f (x) = \sin x \). The curves of anti-derivatives for this function are plotted in will be of the form

\[
F ( x ) = − \cos x + C
\]

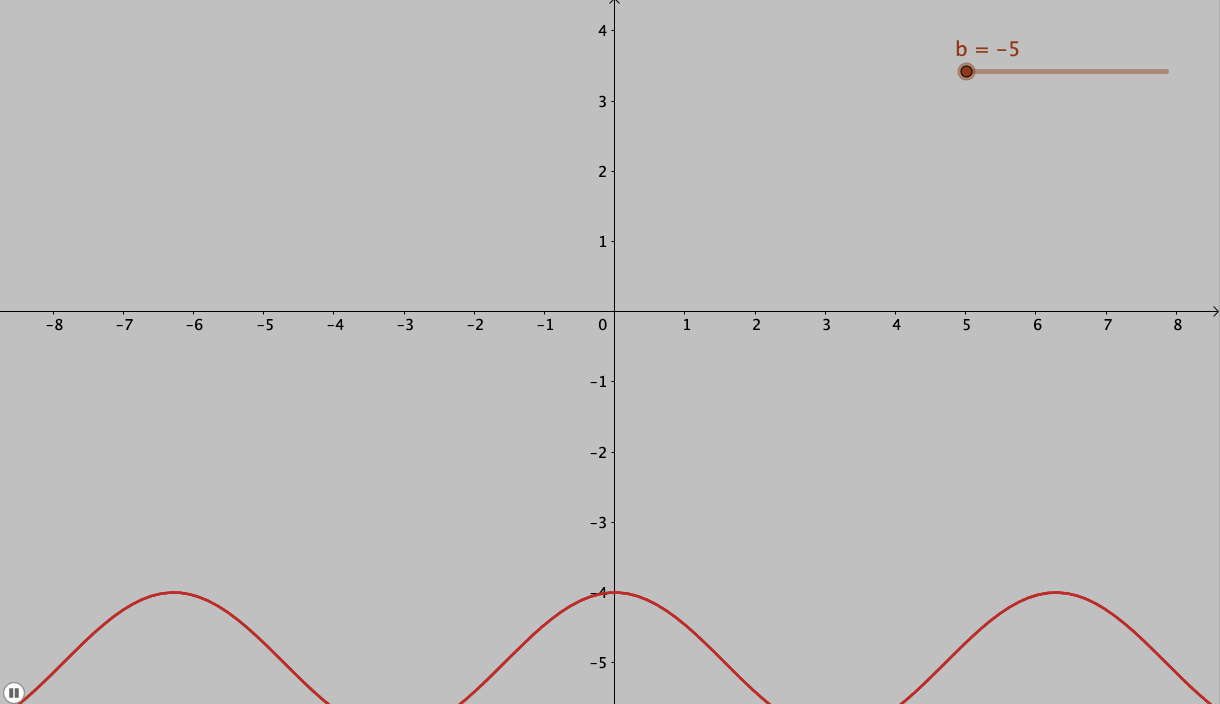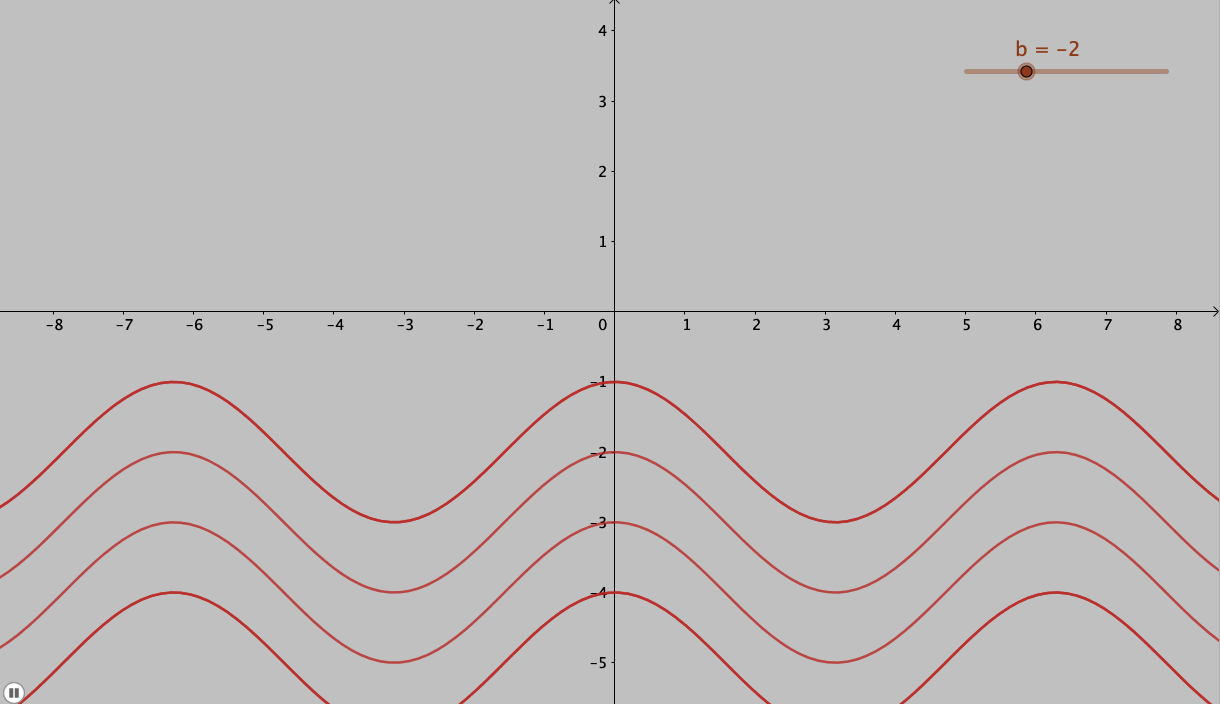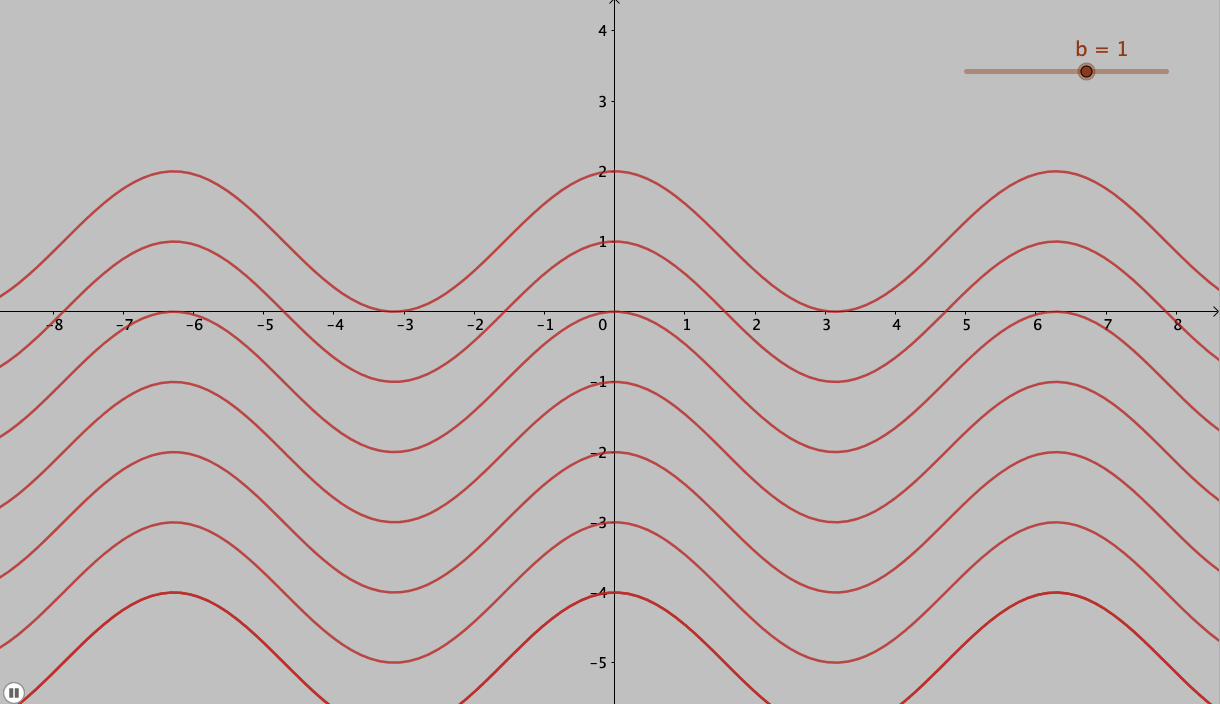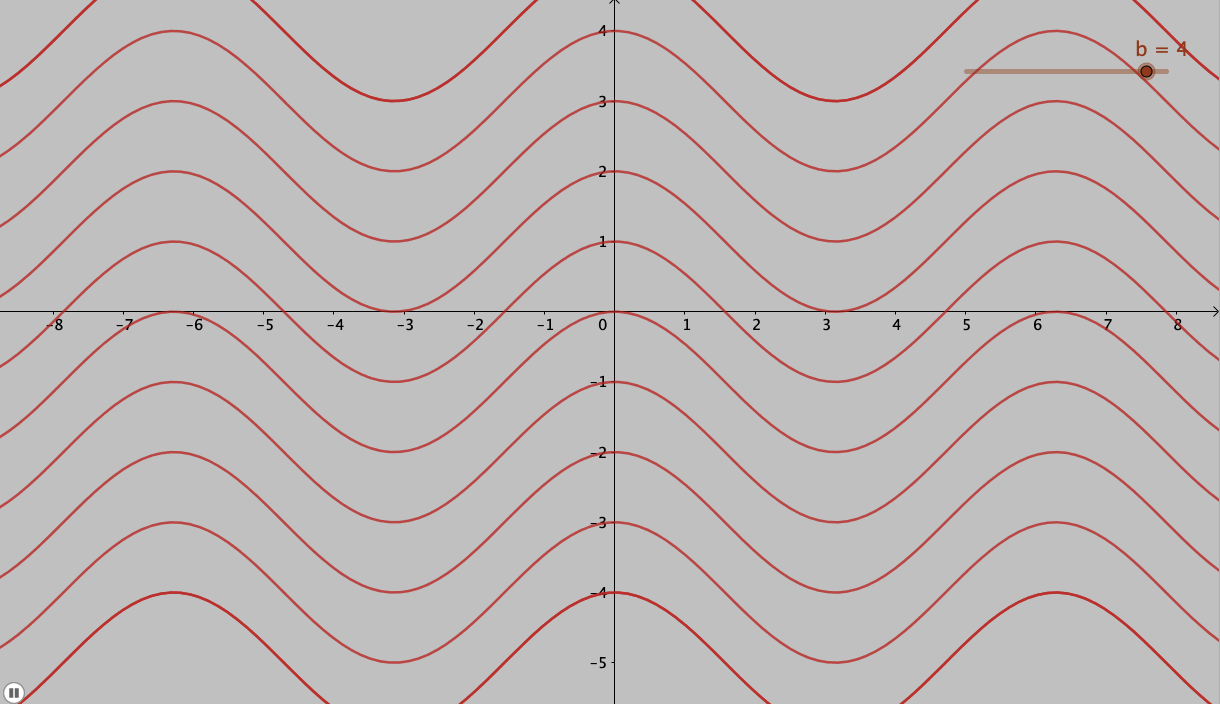
A family of curves of the anti-derivatives of the function \( f (x) = \sin x = –  \cos x \)

And this is the reason for adding the arbitrary constant \( C\) to our result of the anti-derivative: we get a family of curves and the solution is not unique.

Now can we ever know the value of \( C\)? Of course we can, but for this we need to know the some other information about the problem at hand. These can be initial conditions (values) of the variables or the boundary condition. Once we know these we can determine a particular curve (particular solution) from the family of curves for that given problem.

Further Reading

Lev Tarasov – Calculus – Basic Concepts For High Schools (Starts with and explains  the basic mathematical concepts required to understand calculus. The book is in the form of a dialogue between the author and the student, where doubts, misconceptions and aha moments are discussed.)

Morris Kline – Calculus – A physical and intuitive approach (Builds the concepts in the context of the physical problems that calculus was invented to solve.  A book every physics student should read to get an understanding of how mathematics helps solve physical problems.)

Richard  Courant and Fritz John – Introduction to Calculus Analysis (In 2 Volumes) (Standard college level text with in-depth discussions. First volume is rigorous with basic concepts required to conceptually understand the topics and their applications/implications.)

The Mitr

Bertrand Russel’s proof of naïve realism being false

What is naïve realism you may ask? To put simply naïve realism is a belief that whatever you see with your senses is the reality. There is nothing more to reality than what your sense perceptions bring to you. It is a direct unmediated access to reality. There is no “interpretation” involved.

In philosophy of perception and philosophy of mind, naïve realism (also known as direct realism, perceptual realism, or common sense realism) is the idea that the senses provide us with direct awareness of objects as they really are. When referred to as direct realism, naïve realism is often contrasted with indirect realism.

Naïve Realism

To put this in other words, naïve realism fails to distinguish between the phenomenal and the physical object. That is to say, all there is to the world is how we perceive it, nothing more.

Bertrand Russel gave a one line proof of why naïve realism is false. And this is the topic of this post. Also, the proof has some implications for science education, hence the interest.

Naive realism leads to physics, and physics, if true, shows that naive realism is false. Therefore naive realism, if true, is false; therefore it is false.

As quoted in Mary Henle – On the Distinction Between the Phenomenal and the Physical Object, John M. Nicholas (ed.), Images, Perception, and Knowledge, 187-193. (1977)

Henle in her rather short essay (quoted above) on this makes various philosophically oriented arguments to show that it is an easier position to defend when we make a distinction between the two.

But considering the “proof” of Russel, I would like to bring in evidence from science education which makes it even more compelling. There is a very rich body of literature on the theme of misconceptions or alternative conceptions among students and even teachers. Many of these arise simply because of a direct interpretation of events and objects around us.

Consider a simple example of Newton’s first law of motion.

In an inertial frame of reference, an object either remains at rest or continues to move at a constant velocity, unless acted upon by a force.

Now for the naïve realists this will never be possible, as they will never see an object going by itself without application of any force. In real world, friction will bring to halt bodies which are moving. Similar other examples from the misconceptions also do fit in this pattern. This is perhaps so because most of the science is counter-intuitive in nature. With our simple perception we can only do a limited science (perhaps create empirical laws). So one can perhaps say that learners with alternative conceptions hold naïve realist world-view (to some degree) and the role of science education is to change this.

The Mitr

Reason and Faith – Misconceptions in Science Education

Reason does not work in matters of faith. But it may have a chance at clearing misconceptions.
via Tehelka

Truly so. In case of my field of study, namely science education research, it may be the other way round. The classic studies in science education aim at identifying the misconceptions that the learners have regarding a particular subject and then finding a mechanism by which they could be addressed.
This was a very simple but very basic presentation of  what most studies try to achieve, though the methodology may be different. There are some studies which present us with a conceptual framework so that all the responses and the problems with the learners can be seen in light of a theoretical construct. This they say will enable us to make sense of what we see in the classrooms, and what is present as representation in the learners mind. What I think they are trying to say is that we need to get to the conceptual structures that lead to formation of the misconceptions.
Now mind you that many of these misconceptions in science are very stubborn and people are very reluctant to give them up. The reason may be that many of these misconceptions come from direct factual experience in the real world. And from what I know about Philosophy of Science, we might want to make a case that all science is counter-intuitive to our everyday experience. This would explain why misconceptions in science arise. But would this case explain all the known misconceptions?
Let us do some analysis of how a particular misconception might arise.There can be two different reasons for a misconception to arise, if we adhere to deductive logic. That is to say we assume that we have a set of starting statements that are given, whose authenticity is not questioned. And from these set of statements we make certain deductions regarding the world out there. Now there can be two problems with this scenario, one is that the set of statements that we are taking for granted might be wrong, the other is that in the process of deduction that we have followed we made a mistake. The mistake is learnt only when the end result of our analysis is not consistent with the observations in the real world. Or it might be even the case that the so called misconception will lead to a correct answer, at least in some cases.  In these cases we have to resort to more detailed analysis of the thought structure which lead to the answers. Another identifying characteristic of the misconceptions is presence of the inconsistencies across different areas known to the learners. Whereas they might get a particular concept clearly and correctly, in applying same thing for another concept they just might revert to a completely opposite argument and in doing this they do not realise the inconsistency.
We will be clearer on this issue when we talk with a few examples. Suppose that we have a scenario in which we are trying to understand the phenomena of day and night, its causes and consequences. A typical argument in our class goes like this:

How many have seen the Sun set?

Almost all hands would go up, then comes the next question:

How many have seen the Sun rise?

Almost same number of hands go up, excepting a few, who are late risers like me. Some of the more intelligent and the more knowledgeable would say,
“Wait! Sun doesn’t rise and set, it is the Earth that is moving, so it causes the apparent motion of Sun across the sky, the start and end of which we call as day and night. So in conclusion the Sun doesn’t rise and set, it is an illusion created by motion of Earth.”
To this all of the class agrees. This is what they have learned in the text-book, and mind you the text-book represents truth and only truth, nothing else. It is there to dispel your doubts and misconceptions and is made by a committee of experts who are highly knowledgeable about these things. Now let us continue this line of reasoning and ask them the next question in this series.

Does the Moon rise? If so, does it rise everyday?

The responses to this question are mixed. Most of them would say that it does not rise, it is always there, up in the sky. Some would gather courage and say that it does rise.

Does the Moon set?

Again to this the response is mixed, and mostly negative. Most of them are adamant about the ever presence of the moon in the sky. The next question really upsets them

Do the stars rise and set?

Now this question definitely gets a negative response from almost all of them. Even the more knowledgeable ones fall. They have read different parts of the story, but have not connected them. They tell you the following: “No the stars do not move, they are there all the time.” They also tell you that there is something called as the fixed stars and this is in the text-book, which cannot be wrong. And when asked:

Why are we not able to see the stars during the day time?

They tell you “Of course you cannot see the stars during the day time. This is because our Sun, which is also a star, is too bright and the other stars too far away and hence are dim. So our Sun’s brightness, overwhelms the other stars, and hence they are not visible during the day time, but they are there nonetheless. In the night time, since the Sun is no longer visible, the stars become visible. Have you never noticed that during the evening twilight the stars become visible one by one, the brighter ones first. Whereas in the morning the brightest are the last ones to disappear.”
Of course, the things said above and the reasoning given sounds good. So much so that the respondents are convinced that they understand how things work, and have an elaborate reasoning mechanism to explain the observed things, in this case the formation of day and night and appearance / disappearance of stars during night and day respectively.
You ask them:

Don’t you think there is a problem with what you have just said?

“Where is the problem?”, they tell you. “We just explained scientifically how things are in heaven.”
Then you open the Pandora’s box,
“Well you have just said that the Sun doesn’t move really, it is the Earth that moves, and hence we see the apparent Sun rise and Sun set.”
Then they say, “Yes, that is the case. The Sun doesn’t move, but the Earth does.”
You ask, “How do you know this? Do you see that the Earth is moving?”
They say, “The textbook tells us so ” Some of the more knowledgeable ones say that “Galileo proved that the Earth moves and not the Sun. Since we are on Earth, we see only apparent motion of the Sun.”
You say: “But wait, just now you said that the Moon does not move, it is always in the sky. Also you said that the stars do not move, they are there all the time. Now if the Earth moves, then all these bodies should also move, if only, apparently.Then the stars must also move, just like the Sun does, do not forget that Sun is a star too! So other stars should also just set and rise like the Sun, and so should also the Moon!”
Or you can argue just the opposite: “I claim that it is the Sun that moves, Earth does not move. Isn’t it a lot more easier to explain this way, why we do see the Sun moving, because it moves. And we anyway do not see Earth moving! How will disprove me?”
Then the grumbles start. They have never thought about this. They knew the facts, but never connected them. This lead to the misconceptions regarding these things. They were right in parts, but never got a chance to connect the dots, metaphorically speaking.The reason for these misconceptions is the faith in the text-books, but if the text-books fail to perform the job of asking them the right question, where the reasoning alone can get rid of many of the misconceptions.
If we choose the alternative question, of challenging them to disprove that the Earth is stationary, almost most of them are unable to answer the question of disproving that the idea that the Sun moves and not Earth. They would suggest that we can see this from the satellite in the sky (Can we really?).
Most of us take the things for granted and never question many (or as in most cases, any) of them. And many times the facts are something we do not question. We say that “It is a fact.” This statement basically posits that the information which we think is out there can be unquestionable. But there are many flavours of the post-modern philosophy which challenge this position. They think that the facts themselves are relative, that is to say that one culture has different science than another one.  But let us leave this, and come back to our problem of the stars and the Sun and Moon.
Lets put out the postulates for the above arguments and try to deduce deductively the results that were obtained.
Claim 1: Sun doesn’t move.
Claim 2: Earth moves.
Observation 1: We see the Sun moving across the sky daily, it rises and it sets.
Explanation 1:  Since the Earth moves, and the Sun is stationary, we see that Sun moves apparently. This apparent motion of the Sun is seen as the Sunrise and the Sunset by us. This is what causes the day and night.
But we can have Observation 1 explained by another set of claims, which is exactly opposite, namely, that the Earth doesn’t move but the Sun moves.
Claim 3: The Sun moves.
Claim 4: The Earth does not move.
Explanation 2: Since the Earth does not move, and the Sun does, we just see the Sun passing by in the sky, around the Earth. This causes day and night.
We see that Explanations 1 and 2 are both valid for Observation 1, if the claims 1 and 2, 3 and 4 are true then the respective deductions from them, in this case the Explanations 1 and 2 respectively are also true.So in this case the logical deduction is correct, provided that the Claims or assumptions are correct. But this process does not tell you whether the claims themselves are true or not. But both set of assumptions, cannot be true at the same time. Either the Earth moves or it does not, it cannot be in a state of both. If at all we had an explanation which came from these assumptions which did not correspond with the observations, but was logically deducible, then we can question the assumptions or premises as philosophers call them.
Of course, the things said above and the reasoning given sounds good. So much so that the respondents are convinced that they
understand how things work, and have an elaborate reasoning mechanism
We can have one example of this type.
Assumption 5: Stars do not move, there are so called “fixed stars”.
Assumption 5: During the day time the Sun is too bright, as compared to the other stars.
Now in this case combining Assumption 5 (A5) with Observation 1 (Ob1) we would get the following:
Explanation 3: The stars are too dim as compared to Sun, hence we cannot see them during the day time, but they are present. Hence they do not move.
In Explanation 3 (E3) above the deduction has a problem. The deduction does not follow from the assumption. This is the other problem in which we talked about above.
Most of the people who would suggest these responses have mostly no background in astronomy. Even then the basic facts that Earth goes round the Sun and not the other way round are forced upon them, without any critical emphasis on why it is so. Neither are they presented at point with the cognitive struggle of another view point, namely the geo-centric view. So presenting the learners with opportunities that will make them observe things and make sense of the explanations in light of the assumptions that were made, will enhance the reasoning and help them to overcome some of their misconceptions.
But there is another observation which can be made of the skies. And it can be either done in the classroom with the aid of Free Softwares like Stellarium. After the round of above questions, we usually show the class the rising of the stars from the east. In a darkened room with a projector the effect is quite dramatic for those who have not witnessed such a thing before. So you can show the class, just as the Sun rises, all other celestial bodies like the Moon and the stars also must rise and this is an observed fact.
Observation 2: The stars and planets and the Moon also rise and set everyday.
So how do we make sense of this observation, Ob2 in the light of the assumptions that we have.
Assumption 6: Sun is a star.
Explanation 4: We observe that Sun moves during the day, from East to West. Sun is a star, hence all other stars should also move.
Now why this should be the case will be different for the geo-centric and the helio-centric theories. In case of H-C theory the explantion is simple. The Earth moves hence the stars appear to move in the opposite direction. And this applies to all the objects in the sky.
Since the Earth moves all other celestial objects will appear to move. In case of G-C theory we have to make an assumption that the
stars are “fixed” on some imaginary sphere, and the sphere as a whole rotates.
But coming back to the misconceptions, it is just the ad-hoc belief that the stars do not move (“fixed stars”) in conjunctions with another observation that in presence of too bright objects dim objects cannot be seen leads to belief that the stars are immobile and do not rise and set as the Sun does. There is another disconnection from another fact that they know, or are told in the textbooks, that  the apparent movement of the Sun is caused by the actual movement of  the Earth. There is no connection between these two facts which is  made explicit.
We think that providing opportunities for direct observation aided by software, Stellarium in this case, which help in visualizing the movements of celestial bodies will help in developing the skill of reasoning and explaining an observed phenomena.